Question

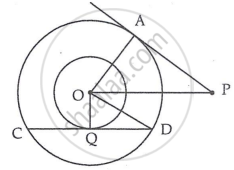
In two concentric circles, the radii are OA = r cm and OQ = 6 cm, as shown in the figure. Chord CD of larger circle is a tangent to smaller circle at Q. PA is tangent to larger circle. If PA = 16 cm and OP = 20 cm, the length CD.

Answer 1

Given that,

OA = r cm, OQ = 6 cm,

PA = 16 cm, OP = 20 cm

In `triangle`AOP,

We have, `angle`OAP = 90°  ...[Radius is perpendicular to tangent at point of contact]

So, OP² = OA² + AP²

⇒ (20)² = r² + (16)² 

⇒ r² = 400 − 256 

⇒ r² = 144

⇒ r = 12cm

Also, OA = OD = 12 cm    ...[Radius of circle]

In `triangle`QOD,

We have, `angle`OQD = 90°    ...[Radius is perpendicular to tangent at point of contact]

So, OD² = OQ² + QD²

⇒ (12)² = (6)² + (QD)²

⇒ QD² = 144 − 36 

⇒ QD² = 108

⇒ QD = `6sqrt3` cm

Also, CD = 2QD  ...[As chord is bisected at the point of contact of circle]

So, CD = `2 × 6sqrt3`

= `12sqrt3` cm

Hence, the length of CD is `12sqrt3` cm.