Advertisements
Advertisements
प्रश्न
In the given figure, you see the frame of a lampshade. It is to be covered with a decorative cloth. The frame has a base diameter of 20 cm and height of 30 cm. A margin of 2.5 cm is to be given for folding it over the top and bottom of the frame. Find how much cloth is required for covering the lampshade.
`["Assume "pi=22/7]`

उत्तर
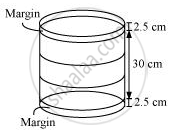
Height (h) of the frame of lampshade = (2.5 + 30 + 2.5) cm = 35 cm
Radius (r) of the circular end of the frame of lampshade = (20/2)cm = 10cm
Cloth required for covering the lampshade = 2πrh
`=(2xx22/7xx10xx35)cm^2`
= 2200 cm2
Hence, for covering the lampshade, 2200 cm2 cloth will be required.
APPEARS IN
संबंधित प्रश्न
The total surface area of a hollow cylinder which is open from both sides is 4620 sq. cm, area of base ring is 115.5 sq. cm and height 7 cm. Find the thickness of the cylinder.
Find the length of 13.2 kg of copper wire of diameter 4 mm, when 1 cubic cm of copper weighs 8.4 gm.
The ratio between the radius of the base and height of a cylinder is 2 : 3. If its volume is 1617 cm3, find the total surface area of the cylinder.
Radius of base of a cylinder is 20 cm and its height is 13 cm, find its curved surface area and total surface area. (π = 3.14)
Find the area of the sheet required to make a cylindrical container which is open at one side and whose diameter is 28 cm and height is 20 cm. Find the approximate area of the sheet required to make a lid of height 2 cm for this container.
The curved surface area of a cylinder is 198cm2 and its base has diameter 21cm. Find the height and the volume of the cylinder.
A well with 6 m diameter is dug. The earth taken out of it is spread uniformly all around it to a width of 2 m to form an embankment of height 2.25 m. Find the depth of the well.
A cylindrical roller 2.5 m in length, 1.75 m in radius when rolled on a road was found to cover the area of 5500 m2. How many revolutions did it make?
In the example given below, the radius of the base of a cylinder and its height is given. Then find the curved surface area and total surface area.
r = 1.4 cm, h = 2.1 cm
In the example given below, the radius of the base of a cylinder and its height is given. Then find the curved surface area and total surface area.
r = 4.2 cm, h = 14 cm
