Advertisements
Advertisements
Question
In the given figure, you see the frame of a lampshade. It is to be covered with a decorative cloth. The frame has a base diameter of 20 cm and height of 30 cm. A margin of 2.5 cm is to be given for folding it over the top and bottom of the frame. Find how much cloth is required for covering the lampshade.
`["Assume "pi=22/7]`

Solution
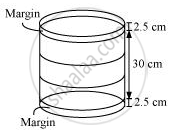
Height (h) of the frame of lampshade = (2.5 + 30 + 2.5) cm = 35 cm
Radius (r) of the circular end of the frame of lampshade = (20/2)cm = 10cm
Cloth required for covering the lampshade = 2πrh
`=(2xx22/7xx10xx35)cm^2`
= 2200 cm2
Hence, for covering the lampshade, 2200 cm2 cloth will be required.
APPEARS IN
RELATED QUESTIONS
A metal pipe is 77 cm long. The inner diameter of a cross section is 4 cm, the outer diameter being 4.4 cm.(See the given figure)

(i) inner curved surface area,
(ii) outer curved surface area,
(iii) total surface area.
`["Assume "pi=22/7]`
A cylindrical pillar is 50 cm in diameter and 3.5 m in height. Find the cost of painting the curved surface of the pillar at the rate of 12.50 per `m^2`.
A solid cylinder has total surface area of 462 cm2. Its curved surface area is one-third of its total surface area. Find the radius and height of the cylinder.
A rectangular strip 25 cm × 7 cm is rotated about the long side. Find The total surface area of the solid thus generated.
Find the curved surface area whose height is 15 cm and the radius of the base is 7 cm.
A rectangular sheet of paper, 44 cm × 20 cm, is rolled along its length of form a cylinder. Find the volume of the cylinder so formed.
The sum of the radius of the base and height of a solid cylinder is 37 m. If the total surface area of the solid cylinder is 1628 cm2. Find the volume of the cylinder.
The ratio between the radius of the base and height of a cylinder is 2 : 3. If its volume is 1617 cm3, find the total surface area of the cylinder.
A solid iron cylinder has total surface area of 1848 sq.m. Its curved surface area is five – sixth of its total surface area. Find the radius and height of the iron cylinder.
A cylindrical roller 2.5 m in length, 1.75 m in radius when rolled on a road was found to cover the area of 5500 m2. How many revolutions did it make?
