Advertisements
Advertisements
प्रश्न
In a harbour, wind is blowing at the speed of 72 km/h and the flag on the mast of a boat anchored in the harbour flutters along the N-E direction. If the boat starts moving at a speed of 51 km/h to the north, what is the direction of the flag on the mast of the boat?
Advertisements
उत्तर १
Velocity of the boat, vb = 51 km/h
Velocity of the wind, vw = 72 km/h
The flag is fluttering in the north-east direction. It shows that the wind is blowing toward the north-east direction. When the ship begins sailing toward the north, the flag will move along the direction of the relative velocity (vwb) of the wind with respect to the boat
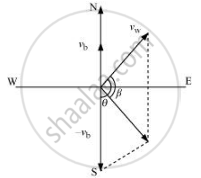
The angle between vw and (–vb) = 90° + 45°
`tanbeta = (51sin(90+45))/(72+51cos (90+45))`
`=(51sin45)/(72+51(-cos45)) = (51xx1/sqrt2)/(72-51xx1/sqrt2)`
`= 51/(72sqrt2-51) = 51/(72xx1.414 - 51) = 51/50.800`
`:.beta = tan^(-1) (1.0038) = 45.11^@`
Angle with respect to the east direction = 45.11° – 45° = 0.11°
Hence, the flag will flutter almost due east.
उत्तर २
When the boat is anchored in the harbour, the flag flutters along the N-E direction. It shows that the velocity of wind is along the north-east direction. When the boat starts moving, the flag will flutter along the direction of relative velocity of wind w.r.t. boat. Let Vwb be the relative velocity of wind w.r.t. boat and P be the angle between Vwb and vw (see fig. below)
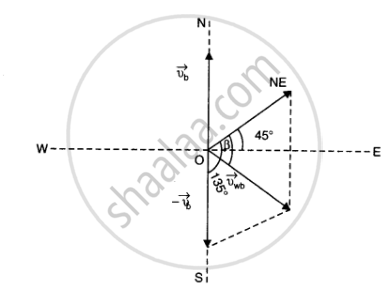
Now `vecv_(wb) = vecv_w + (-vecv_b)`
Here `|vecv_w| = 72 km/h`
`|-vecv_b| = 51 km/h`
Angle between `vecv_w` and `-vecV_b` is 135^@. Then
`tan beta = (51 sin135^@)/(72+51cos135^@) = (51 sin 45^@)/(72+51(-cos 45^@))`
= `(51xx(1/sqrt2))/(72-51(1/sqrt2)) = 1.0039`
`:.beta = tan^(-1) (1.0039) = 45.1^@`
Angle w.r.t east direction = `45.1^@ - 45^@ = 0.1^@`
It means the flag will flutter almost due east.
उत्तर ३
When the boat is anchored in the harbour, the flag flutters along the N-E direction. It shows that the velocity of wind is along the north-east direction. When the boat starts moving, the flag will flutter along the direction of relative velocity of wind w.r.t. boat. Let Vwb be the relative velocity of wind w.r.t. boat and P be the angle between Vwb and vw (see fig. below)
Now `vecv_(wb) = vecv_w + (-vecv_b)`
Here `|vecv_w| = 72 km/h`
`|-vecv_b| = 51 km/h`
Angle between `vecv_w` and `-vecV_b` is 135^@. Then
`tan beta = (51 sin135^@)/(72+51cos135^@) = (51 sin 45^@)/(72+51(-cos 45^@))`
= `(51xx(1/sqrt2))/(72-51(1/sqrt2)) = 1.0039`
`:.beta = tan^(-1) (1.0039) = 45.1^@`
Angle w.r.t east direction = `45.1^@ - 45^@ = 0.1^@`
It means the flag will flutter almost due east.
संबंधित प्रश्न
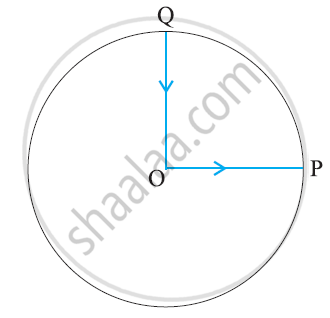
A cyclist starts from the centre O of a circular park of radius 1 km, reaches the edge P of the park, then cycles along the circumference, and returns to the centre along QO as shown in figure. If the round trip takes 10 min, what is the (a) net displacement, (b) average velocity, and (c) average speed of the cyclist?
On an open ground, a motorist follows a track that turns to his left by an angle of 60° after every 500 m. Starting from a given turn, specify the displacement of the motorist at the third, sixth and eighth turn. Compare the magnitude of the displacement with the total path length covered by the motorist in each case.
For any arbitrary motion in space, state whether the following statement is true:
`"V"_"average"` = [r(t2) - r(t1) ] /(t2 – t1)
For any arbitrary motion in space, state whether the following statement is true:
v (t) = v (0) + a t
(The ‘average’ stands for average of the quantity over the time interval t1 to t2)
For any arbitrary motion in space, state whether the following statement is true:
`"r"("t") = "r"(0) + "v"(0)"t" + 1/2 "a" "t"^2 `
(The ‘average’ stands for average of the quantity over the time interval t1 to t2)
In a two dimensional motion, instantaneous speed v0 is a positive constant. Then, which of the following are necessarily true?
In a two dimensional motion, instantaneous speed v0 is a positive constant. Then which of the following are necessarily true?
In a two dimensional motion, instantaneous speed v0 is a positive constant. Then which of the following are necessarily true?
Motion in two dimensions, in a plane can be studied by expressing position, velocity and acceleration as vectors in cartesian co-ordinates A = `A_xhati + A_yhatj` where `hati` and `hatj` are unit vector along x and y directions, respectively and Ax and Ay are corresponding components of (Figure). Motion can also be studied by expressing vectors in circular polar co-ordinates as A = `A_rhatr + A_θhatθ` where `hatr = r/r = cos θhati + sin θj` and `hatθ = - sin θhati + cos θ hatj` are unit vectors along direction in which `r` and `θ` are increasing.
- Express `hati` and `hatj` in terms of `hatr` and `hatθ`
- Show that both `hatr` and `hatθ` are unit vectors and are perpendicular to each other.
- Show that `d/(dt) (hatr) = ωhatθ` where `θ = (dθ)/(dt)` and `d/(dt) (hatθ) = - ωhatr`
- For a particle moving along a spiral given by `t = aθhatr`, where a = 1 (unit), find dimensions of ‘a’.
- Find velocity and acceleration in polar vector representation for particle moving along spiral described in (d) above.
Two balls A and B are placed at the top of 180 m tall tower. Ball A is released from the top at t = 0 s. Ball B is thrown vertically down with an initial velocity 'u' at t = 2 s. After a certain time, both balls meet 100 m above the ground. Find the value of 'u' in ms-1. [use g = 10 ms -2]:
A small toy starts moving from the position of rest under constant acceleration. If it travels a distance of 10 minutes, the distance travelled by the toy in the next will be ______.
Two vectors `vec"A"` and `vec"B"` have equal magnitudes. If magnitude of `vec"A"` + `vec"B"` is equal to two times the magnitude of `vec"A"` - `vec"B"`, then the angle between `vec"A"` and `vec"B"` will be :
A particle of mass 10-2 kg is moving along the positive x-axis under the influence of a force F(x) = `-"K"/(2x)^2` where K = 10-2 Nm2. At time t = 0 it is at x = 1.0 m and its velocity is v = 0. The velocity of particle will be ______ m/s, when it reaches x = 0.50 m.
A displacement vector, at an angle of 30° with y-axis has an x-component of 10 units. Then the magnitude of the vector is ______.
A stone is dropped from the top of the tower and travels 24.5 m in the last second of its journey. The height of the tower is ______.
(g = 9.8 m/s2)
The displacement s of a particle depends on time t according to the following relation `s = 1/3t^3 - t^2 + t`. The velocity and displacement of the particle at the instant when its acceleration is zero, are respectively ______.
