Advertisements
Advertisements
प्रश्न
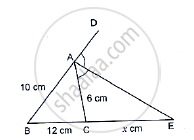
In the following Figure, AE is the bisector of the exterior ∠CAD meeting BC produced in E. If AB = 10cm, AC = 6cm and BC = 12 cm, find CE.
बेरीज
उत्तर
In figure,
AE is the bisector of the exterior ∠CAD.
AB = 10 cm, AC = 6 cm and BC = 12 cm
CE = x
We are aware that the opposite side of a triangle is externally divided by the external bisector of the angle in the ratio of the sides that include the angle. [Theorem of vertical angle bisector]
In ΔABC, AD is the bisector of ∠A.
⇒ `(BE)/(CE) = (AB)/(AC)`
⇒ `(12 + x)/x = 10/6`
⇒ 6(12 + x) = 10x
⇒ 72 + 6x = 10x
⇒ 72 = 10x − 6x
⇒ 72 = 4x
⇒ `72/4` = x
⇒ 18 = x
Therefore, CE = 18 cm
shaalaa.com
या प्रश्नात किंवा उत्तरात काही त्रुटी आहे का?
