Question

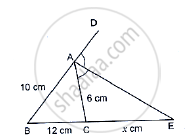
In the following Figure, AE is the bisector of the exterior ∠CAD meeting BC produced in E. If AB = 10cm, AC = 6cm and BC = 12 cm, find CE.

Answer 1

In figure,

AE is the bisector of the exterior ∠CAD.

AB = 10 cm, AC = 6 cm and BC = 12 cm

CE = x

We are aware that the opposite side of a triangle is externally divided by the external bisector of the angle in the ratio of the sides that include the angle. [Theorem of vertical angle bisector] 

In ΔABC, AD is the bisector of ∠A.

⇒ `(BE)/(CE) = (AB)/(AC)`

⇒ `(12 + x)/x = 10/6`

⇒ 6(12 + x) = 10x

⇒ 72 + 6x = 10x

⇒ 72 = 10x − 6x

⇒ 72 = 4x

⇒ `72/4` = x

⇒ 18 = x

Therefore, CE = 18 cm