Advertisements
Advertisements
प्रश्न
In the given fig, XY || seg AC. If 2AX = 3BX and XY = 9. Complete the activity to find the value of AC.
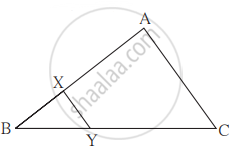
Activity:
2AX = 3BX ...(Given)
∴ `"AX"/"BX" = 3/square`
`("AX" +"BX")/"BX" = (3 + 2)/2` ...(by componendo)
`square/"BX" = 5/2` ...(I)
Now ΔBCA ~ ΔBYX ...`(square" test of similarity")`
∴ `"BA"/"BX" = "AC"/"XY"` ...(Corresponding sides of similar triangles)
∴ `square/square = "AC"/9` ...[From(I)]
∴ AC = `square`
उत्तर
2AX = 3BX ...(Given)
∴ \[\frac{{\text{AX}}}{\text{BX}}\] = \[\frac{3}{\boxed{2}}\]
`("AX" +"BX")/"BX" = (3 + 2)/2` ...(by componendo)
\[\frac{\boxed{\text{AB}}}{\text{BX}}\] = \[\frac{5}{{2}}\] ...(I)
Now ΔBCA ~ ΔBYX ...\[(\boxed{\text{AA}}\text{ test of similarity}\])
∴ `"BA"/"BX" = "AC"/"XY"` ...(Corresponding sides of similar triangles)
∴ \[\frac{\boxed{5}}{\boxed{2}}\] = \[\frac{{\text{AC}}}{9}\] ...[From(I)]
∴ AC = \[\boxed{22.5}\]
