Question

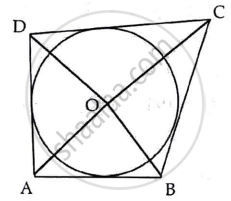
In the given figure, AB, BC, CD and DA are tangents to the circle with centre O forming a quadrilateral ABCD. 

Show that ∠AOB + ∠COD = 180°

Answer 1

Given A quad. ABCD circumscribes a circle with centre O.

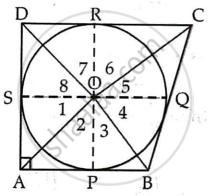
To Prove: 

∠AOB + ∠COD = 180°

and ∠AOD + ∠BOC = 180°

Join OP, OQ, OR and OS.

Tangents formed from a circle's peripheral points form equal angles at its centre. 

∴ ∠1 = ∠2, ∠3 = ∠4, ∠5 = ∠6, ∠7 = ∠8,

And ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8 = 360°    ...[∠s at a Point]

⇒ 2 (∠2 + ∠3) + 2 (∠6 + ∠7) = 360°

2 (∠1 + ∠8) + 2 (∠4 + ∠5) = 360°

⇒ ∠2 + ∠3 + ∠6 + ∠7 = 180°

∠1 + ∠8 + ∠4 + ∠5 = 180°

⇒ ∠AOB + ∠COD = 180°

∠AOD + ∠BOC = 180°