Question

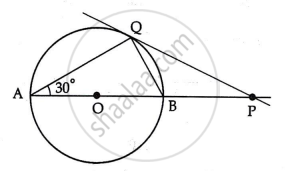
In the given figure, PQ is tangent to a circle centred at O and ∠BAQ = 30°, show that BP = BQ. 

Answer 1

∠BQP = ∠BAQ       ...(∠s in alternate segment are equal)

⇒ ∠BQP = 30°      ...(∵ ∠BAQ = 30° given)      ...(i)

As AB is a diameter, AQB is a Semicircle.

∠AQB = 90°     ...(angle in semicircle = 90°)

From Fig. ∠AQP = ∠AQB + ∠BQP 

⇒ ∠AQP = 90° + 30°

∠AQP = 120°

In ΔAQP,

∠QPA + ∠BAQ + ∠AQP = 180°

⇒ ∠QPA = 30° + 120°

∠QPA = 180°

⇒ ∠QPA = 180 − (30° +120°) 

⇒ ∠QPA = 30°       ...(ii)

From (i) and (ii) we get

∠BQP = ∠QPB = 30°

Therefore, QB = BP