Advertisements
Advertisements
प्रश्न
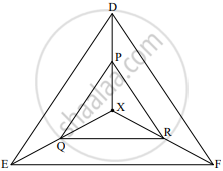
In the given figure, X is any point in the interior of the triangle. Point X is joined to the vertices of triangle. seg PQ || seg DE, seg QR || seg EF. Complete the activity and prove that seg PR || seg DF.
Proof:
In ΔXDE, PQ || DE ......(Given)
∴ `"XP"/"PD" = square/"QE"` ......(Basic proportionality theorem)…(i)
In ΔXEF, QR || EF ......(Given)
∴ `"XQ"/square = "XR"/square` ..........(`square`)....(ii)
∴ `"XP"/"PD" = square/square` ......[From (i) and (ii)]
∴ seg PR || seg DF ......(By converse of basic proportionality theorem
उत्तर
In ΔXDE, PQ || DE ......(Given)
∴ `"XP"/"PD" = "XQ"/"QE"` ......(Basic proportionality theorem)…(i)
In ΔXEF, QR || EF …(Given)
∴ `"XQ"/"QE" = "XR"/"RF"` ........(Basic proportionality theorem)....(ii)
∴ `"XP"/"PD" = "XR"/"RF"` ......[From (i) and (ii)]
∴ seg PR || seg DF ......(By converse of basic proportionality theorem