Advertisements
Advertisements
प्रश्न
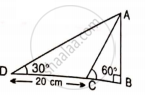
In trapezium ABCD, as shown, AB // DC, AD = DC = BC = 20 cm and A = 60°. Find: distance between AB and DC.
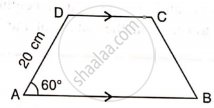
उत्तर
First, draw two perpendiculars to AB from point D and C respectively. Since AB || CD therefore PMCD will be a rectangle.
Consider the figure,
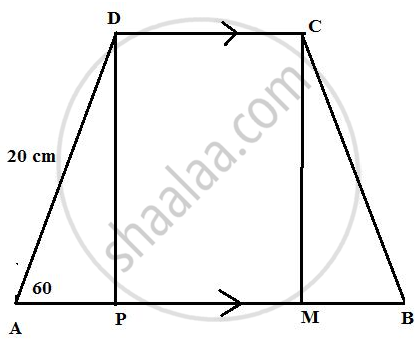
Again from the right triangle APD we have
sin 60° = `"PD"/(20)`
`sqrt(3)/(2) = "PD"/(20)`
PD = `10sqrt(3)`
PD = 10 × 1.732
PD = 17.32
Therefore, the distance between AB and CD is 17.32.
APPEARS IN
संबंधित प्रश्न
Find angle 'A' if :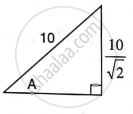
Find angle 'x' if :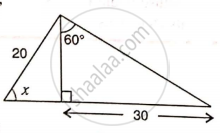
Find the length of AD.
Given: ∠ABC = 60o.
∠DBC = 45o
and BC = 40 cm.
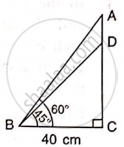
Find the length of AB.
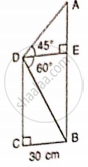
In the given figure, AB and EC are parallel to each other. Sides AD and BC are 2 cm each and are perpendicular to AB.
Given that ∠ AED = 60° and ∠ ACD = 45°. Calculate: AB.
In the given figure, AB and EC are parallel to each other. Sides AD and BC are 2 cm each and are perpendicular to AB.

Given that ∠AED = 60° and ∠ACD = 45°. Calculate: AC
In the given figure, AB and EC are parallel to each other. Sides AD and BC are 2 cm each and are perpendicular to AB.

Given that ∠ AED = 60° and ∠ ACD = 45°. Calculate: AE.
A kite is attached to a 100 m long string. Find the greatest height reached by the kite when its string makes an angles of 60° with the level ground.
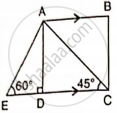
Find AB and BC, if:
If tan x° = `(5)/(12)`,
tan y° = `(3)/(4)` and AB = 48 m; find the length of CD.