Advertisements
Advertisements
प्रश्न
If tan x° = `(5)/(12)`,
tan y° = `(3)/(4)` and AB = 48 m; find the length of CD.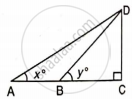
उत्तर
Given tan x° = `(5)/(12)` tan t° = `(3)/(4)` and AB = 48 m;
Let length of BC = x m
From ΔADC
tan x° = `"DC"/"AC"`
`(5)/(12) = "DC"/(48 + x)`
240 + 5x = 12 CD ...(1)
Also, from ΔBDC
tan y° = `"CD"/"BC"`
`(3)/(4) = "CD"/x`
x = `(4"CD")/(3)` ...(2)
From (1)
240 + 5 `((4"CD")/(3))` = 12CD
240 + `(20"CD")/(3)` = 12CD
720 + 20CD = 36CD
16CD = 720
CD = 45
Therefore, length of CD is 45 m.
APPEARS IN
संबंधित प्रश्न
Find 'x', if :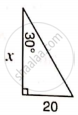
Find angle 'A' if :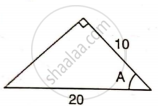
Find angle 'A' if:
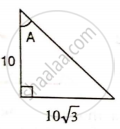
Find angle 'x' if :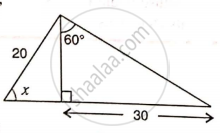
Find the lengths of diagonals AC and BD. Given AB = 60 cm and ∠ BAD = 60°.

Find AB.
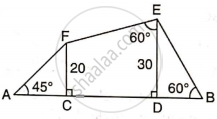
In the given figure, AB and EC are parallel to each other. Sides AD and BC are 2 cm each and are perpendicular to AB.
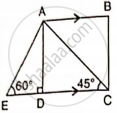
Given that ∠ AED = 60° and ∠ ACD = 45°. Calculate: AB.
In right-angled triangle ABC; ∠ B = 90°. Find the magnitude of angle A, if: AB is √3 times of BC.
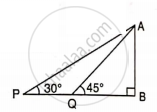
Find PQ, if AB = 150 m, ∠P = 30° and ∠Q = 45°.
.
The perimeter of a rhombus is 96 cm and obtuse angle of it is 120°. Find the lengths of its diagonals.
