Advertisements
Advertisements
प्रश्न
The perimeter of a rhombus is 96 cm and obtuse angle of it is 120°. Find the lengths of its diagonals.
उत्तर
Since in a rhombus all sides are equal.
The diagram is shown below:
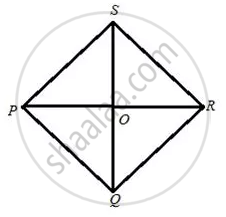
Therefore PQ = `(96)/(4)` = 24 cm, Let ∠PQR = 120°.
We also know that in rhombus diagonals bisect each other perpendicularly and diagonals bisect the angle at vertex.
Hence PQR is a right angle triangle and
PQR = `(1)/(2) ("PQR")` = 60°
sin 60° = `"Perp."/"Hypot." = "PO"/"PQ" = "PO"/(24)`
But
sin 60° = `sqrt(3)/(2)`
`"PO"/(24) = sqrt(3)/(2)`
PO = `12sqrt(3)` = 20.784
Therefore,
PR = 2PO
= 2 × 20.784
= 41.568 cm
Also,
cos 60° = `"Base"/"Hypot" = "OQ"/(24)`
But
cos 60° = `(1)/(2)`
`"OQ"/(24) = (1)/(2)`
OQ = 12
Therefore, SQ = 2 × OQ
= 2 × 12
= 24 cm
So, the length of the diagonal PR = 41.568 cm and SQ = 24 cm.
APPEARS IN
संबंधित प्रश्न
Find 'x', if :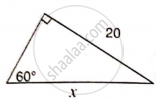
Find angle 'A' if :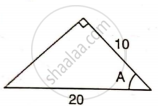
Find angle 'A' if :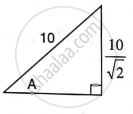
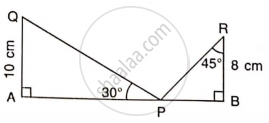
Find the lengths of diagonals AC and BD. Given AB = 60 cm and ∠ BAD = 60°.

Use the information given to find the length of AB.
In the given figure, AB and EC are parallel to each other. Sides AD and BC are 2 cm each and are perpendicular to AB.
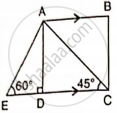
Given that ∠ AED = 60° and ∠ ACD = 45°. Calculate: AB.
In the given figure, AB and EC are parallel to each other. Sides AD and BC are 2 cm each and are perpendicular to AB.

Given that ∠AED = 60° and ∠ACD = 45°. Calculate: AC
A kite is attached to a 100 m long string. Find the greatest height reached by the kite when its string makes an angles of 60° with the level ground.
Find AB and BC, if:
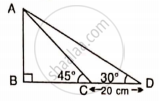
Find AB and BC, if: