Advertisements
Advertisements
Question
If tan x° = `(5)/(12)`,
tan y° = `(3)/(4)` and AB = 48 m; find the length of CD.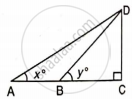
Solution
Given tan x° = `(5)/(12)` tan t° = `(3)/(4)` and AB = 48 m;
Let length of BC = x m
From ΔADC
tan x° = `"DC"/"AC"`
`(5)/(12) = "DC"/(48 + x)`
240 + 5x = 12 CD ...(1)
Also, from ΔBDC
tan y° = `"CD"/"BC"`
`(3)/(4) = "CD"/x`
x = `(4"CD")/(3)` ...(2)
From (1)
240 + 5 `((4"CD")/(3))` = 12CD
240 + `(20"CD")/(3)` = 12CD
720 + 20CD = 36CD
16CD = 720
CD = 45
Therefore, length of CD is 45 m.
APPEARS IN
RELATED QUESTIONS
Find angle 'A' if :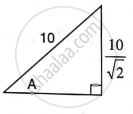
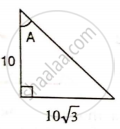
Find angle 'A' if:
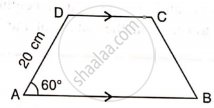
In trapezium ABCD, as shown, AB // DC, AD = DC = BC = 20 cm and A = 60°. Find: distance between AB and DC.
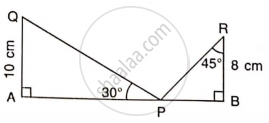
Use the information given to find the length of AB.
In the given figure, AB and EC are parallel to each other. Sides AD and BC are 2 cm each and are perpendicular to AB.
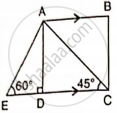
Given that ∠ AED = 60° and ∠ ACD = 45°. Calculate: AB.
In the given figure, AB and EC are parallel to each other. Sides AD and BC are 2 cm each and are perpendicular to AB.

Given that ∠ AED = 60° and ∠ ACD = 45°. Calculate: AE.
Find: AD
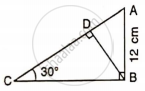
Find AB and BC, if:
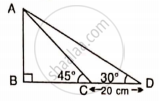
Find AB and BC, if:
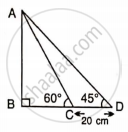
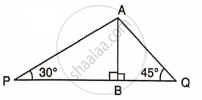
Find PQ, if AB = 150 m, ∠ P = 30° and ∠ Q = 45°.