Advertisements
Advertisements
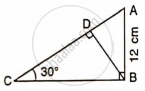
Question
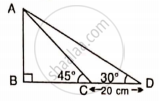
Find AB and BC, if:
Solution
Let BC = x m
BD = BC + CD = (x + 20) cm
In ΔABD,
tan 30° = `"AB"/"BD"`
`(1)/(sqrt(3)) = "AB"/(x + 20)`
x + 20 = `sqrt(3)"AB"` .....(1)
In ΔABC
tan 45° = `"AB"/"BC"`
1 = `"AB"/x`
AB = x ...(2)
From (1)
AB + 20 = `sqrt(3)"AB"`
AB`(sqrt(3)-1) = 20`
AB = `(20)/((sqrt3 - 1))`
= `(20)/((sqrt3 - 1)) xx ((sqrt(3) + 1))/((sqrt(3) + 1))`
= `(20(sqrt(3)+1))/(3 - 1)`
= 27.32cm
From (2)
AB = x = 27.32 cm
Therefore BC = x = AB = 27.32 cm
Therefore, AB = 27.32 cm, BC = 27.32 cm
APPEARS IN
RELATED QUESTIONS
Find 'x', if :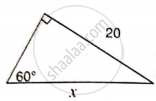
Find 'x', if :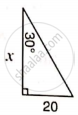
Find the lengths of diagonals AC and BD. Given AB = 60 cm and ∠ BAD = 60°.

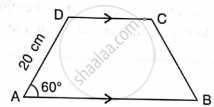
In trapezium ABCD, as shown, AB // DC, AD = DC = BC = 20 cm and ∠ A = 60°. Find: length of AB
In the given figure, AB and EC are parallel to each other. Sides AD and BC are 2 cm each and are perpendicular to AB.
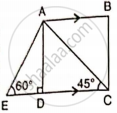
Given that ∠ AED = 60° and ∠ ACD = 45°. Calculate: AB.
In the given figure, ∠B = 60°, AB = 16 cm and BC = 23 cm,
Calculate:
- BE
- AC
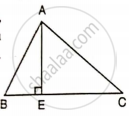
Find: AD
In right-angled triangle ABC; ∠B = 90°. Find the magnitude of angle A, if:
BC is `sqrt(3)` times of AB.
A ladder is placed against a vertical tower. If the ladder makes an angle of 30° with the ground and reaches upto a height of 15 m of the tower; find length of the ladder.
Find PQ, if AB = 150 m, ∠ P = 30° and ∠ Q = 45°.