Advertisements
Advertisements
Question
Find the lengths of diagonals AC and BD. Given AB = 60 cm and ∠ BAD = 60°.

Solution
We know, diagonals of a rhombus bisect each other at right angles and also bisect the angle of the vertex.
The figure is shown below: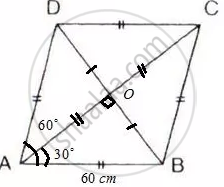
Now
OA = OC =`(1)/(2)`AC, OB = OD =`(1)/(2)`BD; ∠AOB = 90°
And ∠OAB = `(60°)/(2)` = 30°
Also given AB = 60 cm
In right triangle AOB
sin 30° = `"OB"/"AB"`
`(1)/(2) = "OB"/(60)`
OB = 30 cm
Also
cos 30° = `"OA"/"AB"`
`sqrt(3)/(2) = "OA"/60`
OA = 51.96 cm
Therefore,
Length of diagonal AC = 2 x OA = 2 x 51.96 = 103.92 cm.
Length of diagonal BD = 2 x OB = 2 x 30 = 60 cm.
APPEARS IN
RELATED QUESTIONS
Find 'x', if :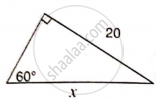
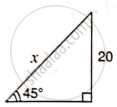
Find 'x', if:
Find angle 'A' if :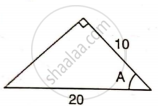
Find AD, if:
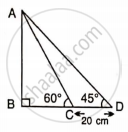
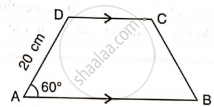
In trapezium ABCD, as shown, AB // DC, AD = DC = BC = 20 cm and ∠ A = 60°. Find: length of AB
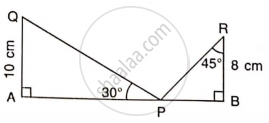
Use the information given to find the length of AB.
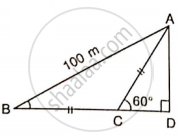
A kite is attached to a 100 m long string. Find the greatest height reached by the kite when its string makes an angles of 60° with the level ground.
Find AB and BC, if:
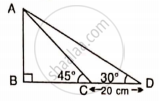
Find AB and BC, if:
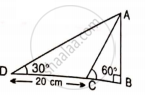
Find AB and BC, if: