Advertisements
Advertisements
Question
Find the length of AD.
Given: ∠ABC = 60o.
∠DBC = 45o
and BC = 40 cm.
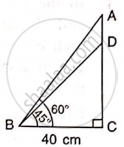
Solution
From right triangle ABC,
tan 60° = `"AC"/"BC"`
⇒ `sqrt(3) = "AC"/40`
⇒ AC = `40sqrt(3)"cm"`
From right triangle BDC,
tan 45° = `"DC"/"BC"`
⇒ 1 = `"DC"/(40)`
⇒ DC = 40 cm
From the figure, it is clear that AD = AC - DC
⇒ AD = `40sqrt(3) - 40`
⇒ AD = `40(sqrt3 - 1)`
⇒ AD = 29.28 cm
APPEARS IN
RELATED QUESTIONS
Find 'x', if :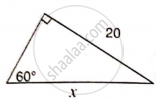
Find angle 'A' if :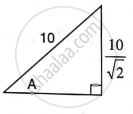
Find AD, if:
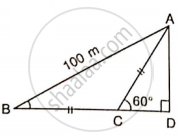
Find the lengths of diagonals AC and BD. Given AB = 60 cm and ∠ BAD = 60°.

In the given figure, AB and EC are parallel to each other. Sides AD and BC are 2 cm each and are perpendicular to AB.
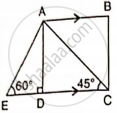
Given that ∠ AED = 60° and ∠ ACD = 45°. Calculate: AB.
Find: AC
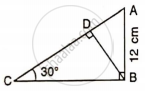
A ladder is placed against a vertical tower. If the ladder makes an angle of 30° with the ground and reaches upto a height of 15 m of the tower; find length of the ladder.
Find AB and BC, if:
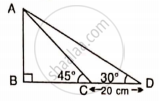
Find AB and BC, if:
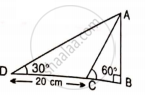
The perimeter of a rhombus is 96 cm and obtuse angle of it is 120°. Find the lengths of its diagonals.
