Advertisements
Advertisements
Question
In the given figure, AB and EC are parallel to each other. Sides AD and BC are 2 cm each and are perpendicular to AB.
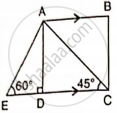
Given that ∠ AED = 60° and ∠ ACD = 45°. Calculate: AB.
Solution
From the triangle ADC we have
tan 45° = `"AD"/"DC"`
1 = `(2)/"DC"`
DC = 2
Since AD || DC and AD⊥EC, ABCD is a parallelogram and hence opposite sides are equal.
Therefore AB = DC = 2 cm.
APPEARS IN
RELATED QUESTIONS
Find 'x', if :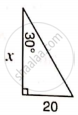
Find angle 'x' if :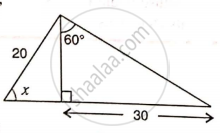
Find AD, if:
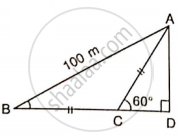
Find the lengths of diagonals AC and BD. Given AB = 60 cm and ∠ BAD = 60°.

Use the information given to find the length of AB.
In the given figure, AB and EC are parallel to each other. Sides AD and BC are 2 cm each and are perpendicular to AB.

Given that ∠AED = 60° and ∠ACD = 45°. Calculate: AC
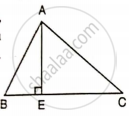
In the given figure, ∠B = 60°, AB = 16 cm and BC = 23 cm,
Calculate:
- BE
- AC
Find: BC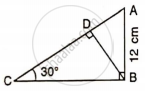
Find AB and BC, if:
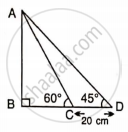
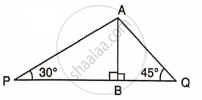
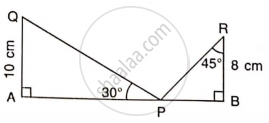
Find PQ, if AB = 150 m, ∠ P = 30° and ∠ Q = 45°.