Advertisements
Advertisements
प्रश्न
It is a well known fact that during a total solar eclipse the disk of the moon almost completely covers the disk of the Sun. From this fact and from the information you can gather from examples 2.3 and 2.4, determine the approximate diameter of the moon.
Advertisements
उत्तर १
The position of the Sun, Moon, and Earth during a lunar eclipse is shown in the given figure.
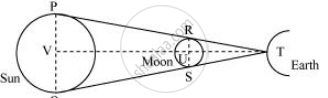
Distance of the Moon from the Earth = 3.84 × 108 m
Distance of the Sun from the Earth = 1.496 × 1011 m
Diameter of the Sun = 1.39 × 109 m
It can be observed that ΔTRS and ΔTPQ are similar. Hence, it can be written as:
`(PQ)/(RS) = (VT)/(UT)`
`(1.39xx10^9)/(RS) = (1.496xx 10^11)/(3.84xx10^(8))`
`RS = (1.39xx3.84)/1.496 xx 10^6 = 3.57 xx10 ^6 m`
Hence, the diameter of the Moon is 3.57× 106 m.
उत्तर २
From examples we get θ = 1920″ and S = 3.8452 x 108 m.
During the total solar eclipse, the disc of the moon completely covers the disc of the sun, so the angular diameter of both the sun and the moon must be equal. Angular diameter of the moon, θ= Angular diameter of the sun
= 1920″ = 1920 x 4.85 x 10-6 rad [1″ = 4.85 x 10-6 rad]
The earth-moon distance, S = 3.8452 x 108 m .’. The diameter of the moon, D = θ x S
= 1920 x 4.85 x 10-6 x 3.8452 x 108 m = 35806.5024 x 102 m
= 3581 x 103 m 3581 km.
संबंधित प्रश्न
Round up the following upto three significant figures:
0.04597
Round up the following upto three significant figures:
2808
How many significant figures should be present in the answer of the following calculation?
0.0125 + 0.7864 + 0.0215
The relative density of lead is 11.3. Its density is ______ g cm–3or ______ kg m–3.
The mean diameter of a thin brass rod is to be measured by vernier callipers. Why is a set of 100 measurements of the diameter expected to yield a more reliable estimate than a set of 5 measurements only?
A man walking briskly in rain with speed v must slant his umbrella forward making an angle θ with the vertical. A student derives the following relation between θ and v: tan θ = v and checks that the relation has a correct limit: as v →0, θ → 0, as expected. (We are assuming there is no strong wind and that the rain falls vertically for a stationary man). Do you think this relation can be correct? If not, guess the correct relation.
State the number of significant figures in the following:
0.0006032 m2
Just as precise measurements are necessary in science, it is equally important to be able to make rough estimates of quantities using rudimentary ideas and common observations. Think of ways by which you can estimate the following (where an estimate is difficult to obtain, try to get an upper bound on the quantity):-
the wind speed during a storm
Solve the numerical example.
Nuclear radius R has a dependence on the mass number (A) as R =1.3 × 10-16 A1/3 m. For a nucleus of mass number A = 125, obtain the order of magnitude of R expressed in the meter.
Solve the numerical example.
Write down the number of significant figures in the following: 0.003 m2, 0.1250 gm cm-2, 6.4 x 106 m, 1.6 x 10-19 C, 9.1 x 10-31 kg.
Answer the following question.
Describe what is meant by order of magnitude.
The radius of the circle is 3.12 m. Calculate the area of the circle with regard to significant figures.
Write a short note on the following.
Rounding - off
How many significant figures should be present in the answer of the following calculations?
`(2.5 xx 1.25 xx 3.5)/2.01`
The mass and volume of a body are 4.237 g and 2.5 cm3, respectively. The density of the material of the body in correct significant figures is ______.
Why do we have different units for the same physical quantity?
How many significant figures are present in the measurement 2007 grams?
Which of the following measurements contains exactly two significant figures?
Which of the following statements is correct about significant figures and accuracy?
