Advertisements
Advertisements
Question
It is a well known fact that during a total solar eclipse the disk of the moon almost completely covers the disk of the Sun. From this fact and from the information you can gather from examples 2.3 and 2.4, determine the approximate diameter of the moon.
Advertisements
Solution 1
The position of the Sun, Moon, and Earth during a lunar eclipse is shown in the given figure.
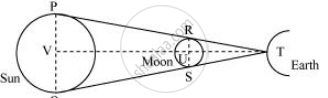
Distance of the Moon from the Earth = 3.84 × 108 m
Distance of the Sun from the Earth = 1.496 × 1011 m
Diameter of the Sun = 1.39 × 109 m
It can be observed that ΔTRS and ΔTPQ are similar. Hence, it can be written as:
`(PQ)/(RS) = (VT)/(UT)`
`(1.39xx10^9)/(RS) = (1.496xx 10^11)/(3.84xx10^(8))`
`RS = (1.39xx3.84)/1.496 xx 10^6 = 3.57 xx10 ^6 m`
Hence, the diameter of the Moon is 3.57× 106 m.
Solution 2
From examples we get θ = 1920″ and S = 3.8452 x 108 m.
During the total solar eclipse, the disc of the moon completely covers the disc of the sun, so the angular diameter of both the sun and the moon must be equal. Angular diameter of the moon, θ= Angular diameter of the sun
= 1920″ = 1920 x 4.85 x 10-6 rad [1″ = 4.85 x 10-6 rad]
The earth-moon distance, S = 3.8452 x 108 m .’. The diameter of the moon, D = θ x S
= 1920 x 4.85 x 10-6 x 3.8452 x 108 m = 35806.5024 x 102 m
= 3581 x 103 m 3581 km.
RELATED QUESTIONS
How many significant figures are present in the 0.0025?
How many significant figures are present in the 500.0?
Round up the following upto three significant figures:
10.4107
How many significant figures should be present in the answer of the following calculation?
5 × 5.364
A student measures the thickness of a human hair by looking at it through a microscope of magnification 100. He makes 20 observations and finds that the average width of the hair in the field of view of the microscope is 3.5 mm. What is the estimate on the thickness of hair?
You are given a thread and a metre scale. How will you estimate the diameter of the thread?
The mean diameter of a thin brass rod is to be measured by vernier callipers. Why is a set of 100 measurements of the diameter expected to yield a more reliable estimate than a set of 5 measurements only?
The photograph of a house occupies an area of 1.75 cm2on a 35 mm slide. The slide is projected on to a screen, and the area of the house on the screen is 1.55 m2. What is the linear magnification of the projector-screen arrangement?
A man walking briskly in rain with speed v must slant his umbrella forward making an angle θ with the vertical. A student derives the following relation between θ and v: tan θ = v and checks that the relation has a correct limit: as v →0, θ → 0, as expected. (We are assuming there is no strong wind and that the rain falls vertically for a stationary man). Do you think this relation can be correct? If not, guess the correct relation.
A LASER is a source of very intense, monochromatic, and unidirectional beam of light. These properties of a laser light can be exploited to measure long distances. The distance of the Moon from the Earth has been already determined very precisely using a laser as a source of light. A laser light beamed at the Moon takes 2.56 s to return after reflection at the Moon’s surface. How much is the radius of the lunar orbit around the Earth?
State the number of significant figures in the following:
0.2370 g cm–3
Solve the numerical example.
The diameter of a sphere is 2.14 cm. Calculate the volume of the sphere to the correct number of significant figures.
Assertion (A): Significant figures for 0.200 is 3 where as for 200 it is 1.
Reason (R): Zero at the end or right of a number are significant provided they are not on the right side of the decimal point.
The sum of the numbers 436.32, 227.2 and 0.301 in appropriate significant figures is ______.
Significant figures in a measurement include which of the following?
What is the least count of a measuring instrument?
How many significant figures are there in the number 0.001405?
Which of the following numbers has 4 significant figures?
A length L is measured as 125 m, which is also written as 12500 cm and 125000 mm. How many significant figures does this measurement have?
