Advertisements
Advertisements
प्रश्न
जैसा चित्र में दिखाया गया है, एक खड़ी होने वाली सीढी के दो पक्षों BA और CA की लम्बाई 1.6m है और इनको A पर कब्जा लगाकर जोड़ा गया है। इन्हें ठीक बीच में 0.5m लम्बी रस्सी DE द्वारा बाँधा गया है। सीढ़ी BA के अनुदिश B से 1.2 m की दूरी पर स्थित बिन्दु F से 40 kg का एक भार लटकाया गया है। यह मानते हुए कि फर्श घर्षणरहित है और सीढी का भार उपेक्षणीय है, रस्सी में तनाव और सीदी पर फर्श द्वारा लगाया गया बल ज्ञात कीजिए।(g =9.8 m/s2 लीजिए)
[संकेत : सीढ़ी के दोनों ओर के संतुलन पर अलग-अलग विचार कीजिए]
उत्तर
माना सीढ़ी के निचले सिरों पर फर्श की प्रतिक्रिया R1 तथा R2 है तथा डोरी का तनाव T है। माना सीढ़ी की दोनों भुजाएँ ऊर्ध्वाधर से कोण से बनाती हैं।
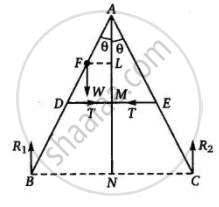
ऊर्ध्वाधर दिशा में संतुलित बलों के कारण `"R"_1 + "R"_2 = "W" = "mg"`
अर्थात `"R"_1 + "R"_2 = 40 "kg" xx 9.8 "m" "s"^-2 = 392 "N"` ...(1)
भुजा AB के घूर्णी संतुलन के लिए बिन्दु A परितः आघूर्ण लेने पर
T . AM + W . FL - R1 . BN = 0 ... (2)
इसी प्रकार भुजा AC के घूर्णी संतुलन के लिए बिन्दु A परितः आघूर्ण लेने पर -
`"R"_2 "NC" - "T". "AM" = 0` ...(3)
∵ DM = DE/2 = 0.5 m
तथा AD = AB/2 = 1.6 m
∴ ΔADM में, `"sin " θ = "DM"/"AD" = 0.25/0.8 = 0.3125`
∴ θ = sin-1 (0.3125) = 18°
cos θ = cos 18° = 0.95 तथा tan θ = tan 18° = 0.33
समीकरण (3) से,
`"T" = "R"_2("NC"/"AM") = "R"^_ (("AC" "sin" theta)/("AE" "cos" theta)) = "R"_2((2"AE")/("AE") "tan" theta)`
= 2R2 × 0.33 = 0.66 R2
समीकरण (2) से,
T . AD cos θ + W . AF sin θ - R1 . AB sin θ = 0
T × 0.8 cos θ + W × 0.4 sin θ - R1 × 1.6 sin θ = 0
∵ AF = AB - BF = (1.6 - 1.2) m
0.66 R2 × 0.8 × 0.95 + 392 × 0.4 × 0.3125 - R1 × 1.6 × 0.3125 = 0 (T व W के मान रखने पर)
या 0.5R2 + 49 - 0.5R1 = 0
या 0.5R1 - 0.5R2 = 49
या R1 - R2 = 98 N ...(5)
समीकरण (1) से,
R1 + R2 = 392 N
हल करने पर, R1 = 245 N तथा R2 = 147 N
तथा समीकरण (4) से, T = 0.66 R2 = 97N
अतः रस्सी में तनाव 97 N तथा फर्श द्वारा सीढ़ी की भुजाओं पर आरोपित बल क्रमशः 245 N तथा 147 N है।
