Advertisements
Advertisements
प्रश्न
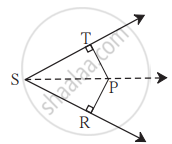
खालील आकृती मध्ये ∠RST = 56°, रेख PT ⊥ किरण ST, रेख PR ⊥ किरण SR आणि रेख PR ≅ रेख PT असेल तर ∠RSP काढा. कारण लिहा.
उत्तर
रेख PT ⊥ किरण ST, रेख PR ⊥ किरण SR ...(पक्ष)
रेख PR ≅ रेख PT
बिंदू P हा ∠TSR चा दुभाजक आहे. ...(कोनाच्या भुजांपासून समान अंतरावर असणारा कोणताही बिंदू त्या कोनाच्या दुभाजकावर असतो.)
∴ किरण SP हा ∠RST चा दुभाजक आहे.
∠RSP = 56° ...(पक्ष)
∴ ∠RSP = `1/2 `∠RST
= `1/2 xx56°`
∴ ∠RSP = 28°
APPEARS IN
संबंधित प्रश्न
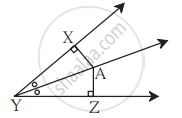
खालील आकृती मध्ये, बिंदू A हा ∠XYZ च्या दुभाजकावर आहे. जर AX = 2 सेमी तर AZ काढा.
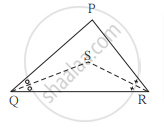
ΔPQR मध्ये जर PQ > PR आणि ∠Q व ∠R चे दुभाजक S मध्ये छेदतात तर दाखवा की, SQ > SR.
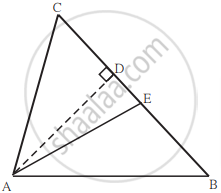
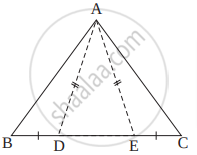
खालील आकृती मध्ये ΔABC च्या BC बाजू वर D आणि E बिंदू असे आहेत की BD = CE तसेच AD = AE तर दाखवा की, ΔABD ≅ ΔACE.
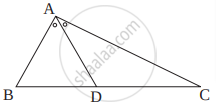
खालील आकृती मध्ये ΔABC च्या ∠BAC चा दुभाजक BC ला D बिंदूत छेदतो, तर सिद्ध करा की AB > BD.
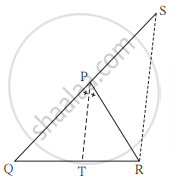
खालील आकृती मध्ये रेख PT हा ∠QPR चा दुभाजक आहे. बिंदू R मधून काढलेली रेख PT ला समांतर असणारी रेषा, किरण QP ला S बिंदूत छेदते, तर सिद्ध करा, PS = PR.
खालील आकृती मध्ये रेख AD ⊥ रेख BC. रेख AE हा ∠CAB चा दुभाजक असून E-D-C. तर दाखवा, की m∠DAE = `1/2` (m∠C - m∠B)