Advertisements
Advertisements
प्रश्न
खालील सारणीत प्रत्येक स्तंभात एक गुणोत्तर दिले आहे. त्यावरून इतर दोन गुणोत्तरे काढा आणि रिकाम्या जागा भरा.
| sin θ | `11/61` | `1/2` | `3/5` | ||||||
| cos θ | `35/37` | `1/sqrt3` | |||||||
| tan θ | `1` | `21/20` | `8/15` | `1/(2sqrt2)` |
उत्तर
| sin θ | `bb(12/37)` | `11/61` | `bb(1/sqrt2)` | `1/2` | `bb(sqrt2/sqrt3)` | `bb(21/29)` | `bb(8/17)` | `3/5` | `bb(1/3)` |
| cos θ | `35/37` | `bb(60/61)` | `bb(1/sqrt2)` | `bb(sqrt3/2)` | `1/sqrt3` | `bb(20/29)` | `bb(15/17)` | `bb(4/5)` | `bb((2sqrt2)/3)` |
| tan θ | `bb(12/35)` | `bb(11/60)` | 1 | `bb(1/sqrt3)` | `bb(sqrt2)` | `21/20` | `8/15` | `bb(3/4)` | `1/(2sqrt2)` |
Explanation:
(i) cos θ = `35/37` ...(i)[पक्ष]
काटकोन ΔABC मध्ये,

∠C = θ
cos θ = `"θ च्या लगतची बाजू"/"कर्ण"`
∴ cos θ = `"BC"/"AC"` ...(ii)
∴ `"BC"/"AC" = 35/37` ...[(i) व (ii) वरून]
∴ BC = 35k आणि AC = 37k मानू
आता, AC2 = AB2 + BC2 ...[पायथागोरसचे प्रमेय]
∴ (37k)2 = AB2 + (35k)2
1369k2 = AB2 + 1225k2
AB2 = 1369k2 – 1225k2
AB2 = 144k2
AB2 = (12k)2
दोन्ही बाजूंचे वर्गमूळ काढून,
AB = 12k
∴ sin θ = `"θ च्या समोरील बाजू"/"कर्ण" = "AB"/"AC" = "12k"/"37k" = 12/37`
tan θ = `"θ च्या समोरील बाजू"/"θ च्या लगतची बाजू" = "AB"/"BC" = "12k"/"35k" = 12/35`
(ii) sin θ = `11/61` ...(i)[पक्ष]
काटकोन ΔABC मध्ये, ∠C = θ
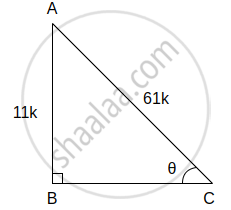
sin θ = `"θ च्या समोरील बाजू"/"कर्ण"`
∴ sin θ = `"AB"/"AC"` ...(ii)
∴ `"AB"/"AC" = 11/61` ...[(i) व (ii) वरून]
∴ AB = 11k आणि AC = 61k मानू
आता, AC2 = AB2 + BC2 ...[पायथागोरसचे प्रमेय]
∴ (61k)2 = (11k)2 + BC2
∴ 3721k2 = 121k2 + BC2
∴ BC2 = 3721k2 – 121k2
∴ BC2 = 3600k2
∴ BC2 = (60k)2
दोन्ही बाजूंचे वर्गमूळ काढून,
BC = 60k
∴ cos θ = `"θ च्या लगतची बाजू"/"कर्ण" = "BC"/"AC" = "60k"/"61k" = 60/61`
tan θ = `"θ च्या समोरील बाजू"/"θ च्या लगतची बाजू" = "AB"/"BC" = "11k"/"60k" = 11/60`
(iii) tan θ = 1 ...(i) [पक्ष]
काटकोन ΔABC मध्ये, ∠C = θ

tan θ = `"θ च्या समोरील बाजू"/"θ च्या लगतची बाजू"`
∴ tan θ = `"AB"/"BC"` ...(ii)
∴ `"AB"/"BC" = 1/1` ...[(i) व (ii) वरून]
∴ AB = 1k आणि BC = 1k मानू
आता, AC2 = AB2 + BC2 ...[पायथागोरसचे प्रमेय]
∴ AC2 = k2 + k2
∴ AC2 = 2k2
दोन्ही बाजूंचे वर्गमूळ काढून,
∴ AC = `sqrt2"k"`
∴ sin θ = `"θ च्या समोरील बाजू"/"कर्ण" = "AB"/"AC" = "1k"/(sqrt2"k") = 1/sqrt2`
∴ cos θ = `"θ च्या लगतची बाजू"/"कर्ण" = "BC"/"AC" = "1k"/(sqrt2"k") = 1/sqrt2`
(iv) sin θ = `1/2` ...(i)[पक्ष]
काटकोन ΔABC मध्ये, ∠C = θ
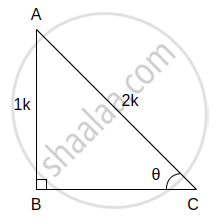
sin θ = `"θ च्या समोरील बाजू"/"कर्ण"`
∴ sin θ = `"AB"/"AC"` ...(ii)
∴ `"AB"/"AC" = 1/2` ...[(i) व (ii) वरून]
∴ AB = 1k आणि AC = 2k मानू
आता, AC2 = AB2 + BC2 ...[पायथागोरसचे प्रमेय]
∴ (2k)2 = k2 + BC2
∴ 4k2 = k2 + BC2
∴ BC2 = 4k2 – k2
∴ BC2 = 3k2
दोन्ही बाजूंचे वर्गमूळ काढून,
∴ BC = `sqrt3"k"`
∴ cos θ = `"θ च्या लगतची बाजू"/"कर्ण" = "BC"/"AC" = (sqrt3"k")/(2"k") = (sqrt3)/2`
tan θ = `"θ च्या समोरील बाजू"/"θ च्या लगतची बाजू" = "AB"/"BC" = (1"k")/(sqrt3"k") = 1/sqrt3`
(v) cos θ = `1/sqrt3` ...(i)[पक्ष]
काटकोन ΔABC मध्ये, ∠C = θ
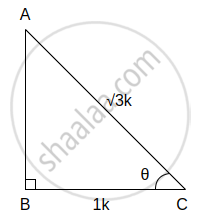
∴ cos θ = `"θ च्या लगतची बाजू"/"कर्ण"`
∴ cos θ = `"BC"/"AC"` ...(ii)
∴ `"BC"/"AC" = 1/sqrt3` ...[(i) व (ii) वरून]
∴ `"AB" = 1"k" "आणि" "BC" = sqrt3"k"` मानू
आता, AC2 = AB2 + BC2 ...[पायथागोरसचे प्रमेय]
`∴ (sqrt3"k")^2 = "AB"^2 + "k"^2`
∴ 3k2 = AB2 – k2
∴ AB2 = 3k2 – k2
∴ AB2 = 2k2
दोन्ही बाजूंचे वर्गमूळ काढून,
AB = `sqrt2`k
∴ sin θ = `"θ च्या समोरील बाजू"/"कर्ण" = "AB"/"AC" = (sqrt2"k")/(sqrt3"k") = sqrt2/sqrt3`
tan θ = `"θ च्या समोरील बाजू"/"θ च्या लगतची बाजू" = "AB"/"BC" = (sqrt2"k")/(1"k") = sqrt2`
(vi) tan θ = `21/20` ...(i) [पक्ष]
काटकोन ΔABC मध्ये, ∠C = θ
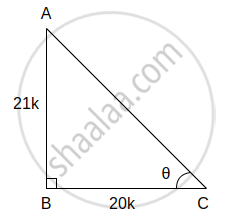
tan θ = `"θ च्या समोरील बाजू"/"θ च्या लगतची बाजू"`
∴ tan θ = `"AB"/"BC"` ...(ii)
∴ `"AB"/"BC" = 21/20` ...[(i) व (ii) वरून]
∴ AB = 21k आणि BC = 20k मानू
आता, AC2 = AB2 + BC2 ...[पायथागोरसचे प्रमेय]
AC2 = (21k)2 + (20k)2
AC2 = 441k2 + 400k2
AC2 = (841k)2
दोन्ही बाजूंचे वर्गमूळ काढून,
AC = 29k
∴ sin θ = `"θ च्या समोरील बाजू"/"कर्ण" = "AB"/"AC" = (21"k")/(29"k") = 21/29`
cos θ = `"θ च्या लगतची बाजू"/"कर्ण" = "BC"/"AC" = (20"k")/(29"k") = 20/29`
(vii) tan θ = `8/15` ...(i)[पक्ष]
काटकोन ΔABC मध्ये, ∠C = θ

tan θ = `"θ च्या समोरील बाजू"/"θ च्या लगतची बाजू"`
∴ tan θ = `"AB"/"BC"` ...(ii)
∴ `"AB"/"BC" = 8/15` ...[(i) व (ii) वरून]
∴ AB = 8k आणि BC = 15k मानू
आता, AC2 = AB2 + BC2 ...[पायथागोरसचे प्रमेय]
∴ AC2 = (8k)2 + (15k)2
∴ AC2 = 64k2 + 225k2
∴ AC2 = (289k)2
दोन्ही बाजूंचे वर्गमूळ काढून,
∴ AC = 17k
∴ sin θ = `"θ च्या समोरील बाजू"/"कर्ण" = "AB"/"AC" = (8"k")/(17"k") = 8/17`
cos θ = `"θ च्या लगतची बाजू"/"कर्ण" = "BC"/"AC" = (15"k")/(17"k") = 15/17`
(viii) sin θ = `3/5` ...(i) [पक्ष]
काटकोन ΔABC मध्ये, ∠C = θ
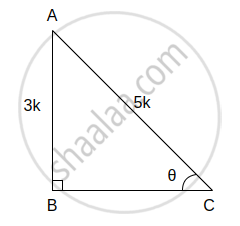
sin θ = `"θ च्या समोरील बाजू"/"कर्ण"`
∴ sin θ = `"AB"/"AC"` ...(ii)
∴ `"AB"/"AC" = 3/5` ...[(i) व (ii) वरून]
∴ AB = 3k आणि AC = 5k मानू
आता, AC2 = AB2 + BC2 ...[पायथागोरसचे प्रमेय]
∴ (5k)2 = (3k)2 + BC2
∴ 25k2 = 9k2 + BC2
∴ BC2 = 25k2 – 9k2
∴ BC2 = 16k2
दोन्ही बाजूंचे वर्गमूळ काढून,
∴ BC = 4k
∴ cos θ = `"θ च्या लगतची बाजू"/"कर्ण" = "BC"/"AC" = (4"k")/(5"k") = 4/5`
tan θ = `"θ च्या समोरील बाजू"/"θ च्या लगतची बाजू" = "AB"/"BC" = (3"k")/(4"k") = 3/4`
(ix) tan θ = `1/(2sqrt2)` ...(i)[पक्ष]
काटकोन ΔABC मध्ये, ∠C = θ
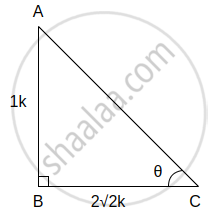
tan θ = `"θ च्या समोरील बाजू"/"θ च्या लगतची बाजू"`
∴ tan θ = `"AB"/"BC"` ...(ii)
∴ `"AB"/"BC" = 1/(2sqrt2)` ...[(i) व (ii) वरून]
∴ AB = 1k आणि BC = `2sqrt2"k"` मानू
आता, AC2 = AB2 + BC2 ...[पायथागोरसचे प्रमेय]
∴ `"AC"^2 = (1"k")^2 + (2sqrt2"k")^2 `
∴ AC2 = 1k2 + 8k2
∴ AC2 = (9k)2
दोन्ही बाजूंचे वर्गमूळ काढून,
∴ AC = 3k
∴ sin θ = `"θ च्या समोरील बाजू"/"कर्ण" = "AB"/"AC" = (1"k")/(3"k") = 1/3`
cos θ = `"θ च्या लगतची बाजू"/"कर्ण" = "BC"/"AC" = (2sqrt2"k")/(3"k") = (2sqrt2)/3`
