Advertisements
Advertisements
प्रश्न
खालील दिलेल्या आकृतीमध्ये ∠PQR = 90°, ∠PQS = 90°, ∠PRQ = α व ∠QPS = θ तर खालील त्रिकोणमितीय गुणोत्तरे लिहा.
- sin α, cos α, tan α
- sin θ, cos θ, tan θ

उत्तर
(i) ∆PQR मध्ये,
sin α = `("∠PQR" "च्या समोरील बाजू")/"कर्ण" = "PQ"/"PR"`
cos α = `("∠PQR" "च्या लगतची बाजू")/"कर्ण" = "RQ"/"PR"`
tan α = `("∠PQR" "च्या समोरील बाजू")/("∠PQR" "च्या लगतची बाजू") = "PQ"/"RQ"`
(ii) ∆PQS मध्ये,
sin θ = `("∠QPS" "च्या समोरील बाजू")/"कर्ण" = "QS"/"PS"`
cos θ = `("∠QPS" "च्या लगतची बाजू")/"कर्ण" = "PQ"/"PS"`
tan θ = `("∠QPS" "च्या समोरील बाजू")/("∠QPS" "च्या लगतची बाजू") = "QS"/"PQ"`
APPEARS IN
संबंधित प्रश्न
खालील आकृती मध्ये ΔPQR चा ∠R हा काटकोन आहे तर खालील गुणोत्तरे लिहा.
- sin P
- cos Q
- tan P
- tan Q

खालील आकृती मध्ये ΔXYZ हा काटकोन त्रिकोण आहे. ∠XYZ = 90° आहे. बाजूंची लांबी a, b, c अशी दिली आहे. यावरून खालील गुणोत्तरे लिहा.
- sin X
- tan Z
- cos X
- tan X

काटकोन ΔLMN मध्ये, ∠LMN = 90°, ∠L = 50° आणि ∠N = 40° आहे. यावरून खालील गुणोत्तरे लिहा.
- sin 50°
- cos 50°
- tan 40°
- cos 40°

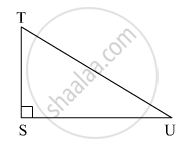
काटकोन ΔTSU मध्ये TS = 5, ∠S = 90°, SU = 12 तर sin T, cos T, tan T काढा. तसेच sin U, cos U, tan U काढा.
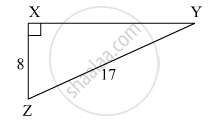
काटकोन ΔYXZ मध्ये, ∠X = 90°, XZ = 8 सेमी, YZ = 17 सेमी तर sin Y, cos Y, tan Y, sin Z, cos Z, tan Z काढा.
काटकोन ΔLMN मध्ये ∠N = θ, ∠M = 90°, cos θ = `24/25` तर sin θ आणि tan θ ही गुणोत्तरे काढा, तसेच (sin2 θ) व (cos2 θ) ची किंमत काढा.

