Advertisements
Advertisements
प्रश्न
किसी आयत का क्षेत्रफल 192 वर्ग सेमी तथा उसकी लंबाई 16 सेमी हो, तो उस आयत के विकर्ण की लंबाई ज्ञात कीजिए।
उत्तर
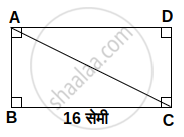
मान लो, `square`ABCD एक दिया गया आयत है।
BC = 16 सेमी,
A(`square`ABCD) = 192 वर्ग सेमी।
आयत का क्षेत्रफल = लंबाई × चौड़ाई
A(`square`ABCD) = AB × BC
∴ 192 = AB × 16
∴ AB = `192/16`
∴ AB = 12 सेमी
ΔABC में, ∠ABC = 90° ...(आयत के कोण)
पायथागोरस प्रमेय से,
AC2 = AB2 + BC2
∴ AC2 = 122 + 162
∴ AC2 = 144 + 256
∴ AC2 = 400
∴ AC = 20 सेमी ...(दोनों पक्षों का वर्गमूल लेने पर)
आयत के विकर्ण की लंबाई 20 सेमी है।
APPEARS IN
संबंधित प्रश्न
आकृति में ∠DFE = 90°, रेख FG ⊥ रेख ED. यदि GD = 8, FG = 12, तो (1) EG (2) FD (3) EF का मान ज्ञात कीजिए।

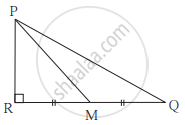
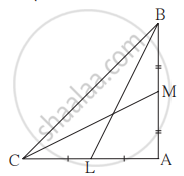
आकृति में M यह भुजा QR का मध्यबिंदु है। ∠PRQ = 90° तो सिद्ध कीजिए कि, PQ2 = 4PM2 - 3PR2
किसी रास्ते के दोनों ओर स्थित घरों की दीवारें एक दूसरे के समांतर हैं। 5.8 मी लंबाई वाली सीढी़ का सिरा रास्ते पर हो और उसका ऊपरी सिरा घर के 4 मीटर ऊँचाई पर स्थित खिड़की तक पहुँचता है। उसी स्थान से सीढी़ को रास्ते के दूसरी ओर झुकाने पर उसका ऊपरी सिरा दूसरे घर के 4.2 मीटर ऊँचाई पर स्थित खिड़की तक पहुँचता हो तो रास्ते की चौड़ाई ज्ञात कीजिए।
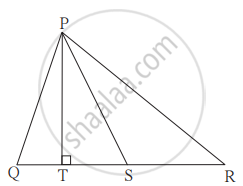
आकृति में रेख PS यह ΔPQR की माध्यिका है और PT ⊥ QR तो सिद्ध कीजिए कि,
(1) PR2 = PS2 + QR × ST + `("QR"/2)^2`
(2) PQ2 = PS2 - QR × ST + `("QR"/2)^2`
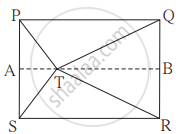
आकृति में दर्शाएनुसार बिंदु T यह आयत PQRS के अंतर्भाग में स्थित है। तो सिद्ध कीजिए कि, TS2 + TQ2 = TP2 + TR2 (आकृति में दर्शाएअनुसार रेख AB || भुजा SR ऐसा खींचिए कि A-T-B)
निम्नलिखित बहुवैकल्पिक प्रश्न के दिए गए उत्तरों में से उचित विकल्प चुनकर लिखिए।
समकोण त्रिभुज में समकोण बनानेवाली भुजाओं के वर्गों का योगफल 169 हो तो उसके कर्ण की लंबाई कितनी होगी?
निम्नलिखित बहुवैकल्पिक प्रश्न के दिए गए उत्तरों में से उचित विकल्प चुनकर लिखिए।
किसी चतुर्भुज का विकर्ण `10sqrt2` सेमी हो तो उसकी परिमिति ______ होगी।
किसी समद्विबाहु समकोण त्रिभुज के भुजा की लंबाई x हो, तो उसके कर्ण की लंबाई ज्ञात कीजिए।
ΔABC में ∠BAC = 90°, रेख BL तथा रेख CM, यह ΔABC की माध्यिकाएँ हों तो सिद्ध कीजिए कि, 4(BL2 + CM2) = 5 BC2
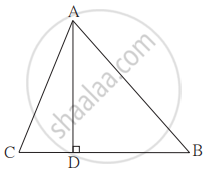
ΔABC में रेख AD ⊥ रेख BC और DB = 3CD, तो सिद्ध कीजिए कि : 2AB2 = 2AC2 + BC2