Advertisements
Advertisements
प्रश्न
किसी समबाहु त्रिभुज की ऊँचाई `sqrt3` सेमी हो, तो उस त्रिभुज के भुजा की लंबाई तथा उसकी परिमिति ज्ञात कीजिए।
उत्तर
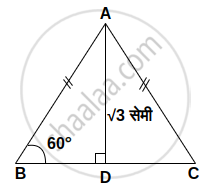
मान लो, ΔABC एक दिया गया समबाहु त्रिभुज है और रेख AD उसकी ऊँचाई है।
AD = `sqrt3` सेमी
∠B = 60° ...(समबाहु त्रिभुज के कोण)
ΔADB में,
∠ADB + ∠ABD + ∠BAD = 180° ...(त्रिभुज के सभी कोणों के मापों का योग)
∴ 90° + 60° + ∠BAD = 180°
∴ 150° + ∠BAD = 180°
∴ ∠BAD = 180° - 150°
∴ ∠BAD = 30°
∴ ΔADB एक 30°- 60° - 90° त्रिभुज है।
AD = `sqrt3/2`AB ...(60° के सम्मुख भुजा)
`sqrt3 = sqrt3/2`AB
∴ AB = `(2 xx sqrt3)/sqrt3`
∴ AB = 2 सेमी
समबाहु त्रिभुज के भुजा की लंबाई 2 सेमी है
ΔABC की परिमिति = 3 × भुजा = 3 × AB
= 3 × 2 = 6 सेमी
समबाहु त्रिभुज की परिमिति 6 सेमी है।
समबाहु त्रिभुज के भुजा की लंबाई 2 सेमी तथा उसकी परिमिति 6 सेमी है।
APPEARS IN
संबंधित प्रश्न
आकृति में ∠DFE = 90°, रेख FG ⊥ रेख ED. यदि GD = 8, FG = 12, तो (1) EG (2) FD (3) EF का मान ज्ञात कीजिए।

किसी आयत की लंबाई 35 सेमी तथा चौड़ाई 12 सेमी हो तो उस आयत के विकर्ण की लंबाई ज्ञात कीजिए।
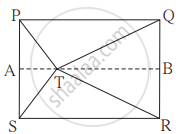
आकृति में दर्शाएनुसार बिंदु T यह आयत PQRS के अंतर्भाग में स्थित है। तो सिद्ध कीजिए कि, TS2 + TQ2 = TP2 + TR2 (आकृति में दर्शाएअनुसार रेख AB || भुजा SR ऐसा खींचिए कि A-T-B)
निम्नलिखित बहुवैकल्पिक प्रश्न के दिए गए उत्तरों में से उचित विकल्प चुनकर लिखिए।
समकोण त्रिभुज में समकोण बनानेवाली भुजाओं के वर्गों का योगफल 169 हो तो उसके कर्ण की लंबाई कितनी होगी?
किसी समकोण त्रिभुज में समकोण बनाने वाली भुजाएँ क्रमश: 9 सेमी तथा 12 सेमी हों तो उस त्रिभुज के कर्ण की लंबाई ज्ञात कीजिए।
किसी समद्विबाहु समकोण त्रिभुज के भुजा की लंबाई x हो, तो उसके कर्ण की लंबाई ज्ञात कीजिए।
किसी आयत का क्षेत्रफल 192 वर्ग सेमी तथा उसकी लंबाई 16 सेमी हो, तो उस आयत के विकर्ण की लंबाई ज्ञात कीजिए।
समलंब चतुर्भुज ABCD में,
रेख AB || रेख DC
रेख BD ⊥ रेख AD,
रेख AC ⊥ रेख BC,
यदि AD = 15, BC = 15 और AB = 25 हो तो A(`square` ABCD) का मान कितना होगा?

यदि a, b, c त्रिभुज की भुजाएँ हैं और a2 + b2 = c2 हो, तो उस त्रिभुज के प्रकार का नाम लिखिए?
यदि वर्ग के विकर्ण की लंबाई 10`sqrt2` सेमी हो, तो उस वर्ग की भुजा की लंबाई ज्ञात कीजिए।
