Advertisements
Advertisements
प्रश्न
किसी बंदरगाह में 72 km/h की चाल से हवा चल रही है और बंदरगाह में खड़ी किसी नौका के ऊपर लगा झंडा N-E दिशा में लहरा रहा है। यदि वह नौका उत्तर की ओर 51 km/h की चाल से गति करना प्रारंभ कर दे तो नौको पर लगा झंडा किस दिशा में लहराएगा?
उत्तर
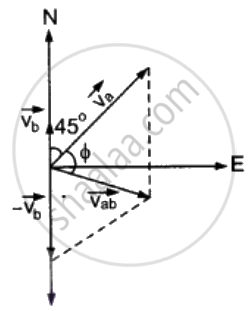
माना वायु का वेग = `vec"v"_"a"` तथा नौका का वेग `vec"v"_"b"`
तब νa = 72 km/h, N-E दिशा में
νb = 51 km/h, उत्तर दिशा में
माना वायु का नौका के सापेक्ष वेग `vec"v"_"ab"` है तो
`vec"v"_"ab" = vec"v"_"a" - vec"v"_"b"`
स्पष्ट है की `vec"v"_"ab"` वायु वेग ` vec"v"_"a"` तथा नौका के विपरीत दिशा वेग ` - vec"v"_"b"` के परिणामी के बराबर है तथा झंडा, वेग `vec"v"_"ab"` की दिशा में ही लहराएगा।
माना वेग `vec"v"_"ab"`, वेग `vec"v"_"a"` से ∅ से कोण बनता है, जबकि वेगों `vec"v"_"a"` तथा ` - vec"v"_"b"` के बीच का कोण θ = 135° है।
∴ सूत्र `"H"_"M" = ("u"^2. "sin"^2theta_0)/(2"g")` से
`25 = [((40)^2 xx "sin"^2 theta_0)/(2 xx 9.8)]`
∴ `"sin"^2 theta_2 = [(25 xx 2 xx 9.8)/ (40)^2] = 0.30625`
अथवा `"sin" theta_0 = sqrt0.30625 = 0.5534`
∴ उक्त प्रक्षेप्य वेग तथा प्रक्षेप्य कोण के लिए अधिकतम क्षैतिज दूरी = क्षैतिज परास R
= `("u"^2. "sin"2 theta_0)/"g" = ("u"^2 (2 "sin "theta_0 . "cos" theta_0))/"g"`
= `("u"^2 . 2 "sin" theta_0 xx sqrt (1-"sin"^2 theta_0))/"g"`
= `[((40)^2 xx 2 xx 0.5534 sqrt(1-0.30625))/9.8]` मी
= `[(40^2 xx 2 xx 0.5534 xx 0.8329)/9.8]` मी
= 150.5 मी
APPEARS IN
संबंधित प्रश्न
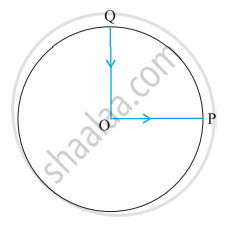
कोई साइकिल सवार किसी वृत्तीय पार्क के केंद्र O से चलना शुरू करता है तथा पार्क के किनारे P पर पहुँचता है। पुनः वह पार्क की परिधि के अनुदिश साइकिल चलाता हुआ QO के रास्ते (जैसा कि चित्र में दिखाया गया है) केंद्र पर वापस आ जाता है। पार्क की त्रिज्या 1 km है। यदि पूरे चक्कर में 10 मिनट लगते हों तो साइकिल सवार का (a) कुल विस्थापन, (b) औसत वेग तथा (c) औसत चाल क्या होगी?
किसी खुले मैदान में कोई मोटर चालक एक ऐसा रास्ता अपनाता है जो प्रत्येक 500 m के बाद उसके बाईं ओर 60° के कोण पर मुड़ जाता है। किसी दिए मोड़ से शुरू होकर मोटर चालक का तीसरे, छठे व आठवें मोड़ पर विस्थापन बताइए। प्रत्येक स्थिति में मोटर चालक द्वारा इन मोड़ों पर तय की गई कुल पथ-लंबाई के साथ विस्थापन के परिमाण की तुलना कीजिए।
कोई व्यक्ति स्थिर जल में 4.0 km/h की चाल से तैर सकता है। उसे 1.0 km चौड़ी नदी को पार करने में कितना समय लगेगा? यदि नदी 3.0 km/h की स्थिर चाल से बह रही हो और वह नदी के बहाव के लंब तैर रहा हो। जब वह नदी के दूसरे किनारे पहुँचता है तो वह नदी के बहाव की ओर कितनी दूर पहुँचेगा?
किसी दिकस्थान पर एक स्वेच्छ गति के लिए निम्नलिखित संबंध सत्य है या नहीं, यह बताइए:
`"v"_"औसत" = (1/2)("v"("t"_1) + "v"("t"_2))`
यहाँ औसत का आशय समय अंतराल t2 व t1 से संबंधित भौतिक राशि के औसत मान से है।
किसी दिकस्थान पर एक स्वेच्छ गति के लिए निम्नलिखित संबंध सत्य है या नहीं, यह बताइए:
`"v"_"औसत" =["r"("t"_2) -"r"("t"_1)]//("t"_2 - "t"_1)`
यहाँ औसत की आशय समय अंतराल t2 व t1 से संबंधित भौतिक राशि के औसत मान से है।
किसी दिक्स्थान पर एक स्वेच्छ गति के लिए निम्नलिखित संबंध सत्य है या नहीं, यह बताइए:
`"v"("t") = "v"(0) + "a" "t"`
यहाँ औसत की आशय समय अंतराल t2 व t1 से संबंधित भौतिक राशि के औसत मान से है।
किसी दिक्स्थान पर एक स्वेच्छ गति के लिए निम्नलिखित संबंध सत्य है या नहीं, यह बताइए:
`"r"("t") = "r"(0) + "v"(0)"t" + 1/2 "a" "t"^2 `
यहाँ औसत की आशय समय अंतराल t2 व t1 से संबंधित भौतिक राशि के औसत मान से है।
किसी दिक्स्थान पर एक स्वेच्छ गति के लिए निम्नलिखित संबंध सत्य है या नहीं, यह बताइए:
`"a"_"औसत" = ["v"("t"_2) - "v"("t"_1)]/("t"_2 - "t"_1)`
यहाँ औसत की आशय समय अंतराल t2 व t1 से संबंधित भौतिक राशि के औसत मान से है।
किसी सदिश में परिमाण व दिशा दोनों होते हैं। क्या दिक़स्थान में इसकी कोई स्थिति होती है? क्या यह समय के साथ परिवर्तित हो सकता है? क्या दिकस्थान में भिन्न स्थानों पर दो बराबर सदिशों a व b का समान भौतिक प्रभाव अवश्य पड़ेगा? अपने उत्तर के समर्थन में उदाहरण दीजिए।
किसी सदिश में परिमाण व दिशा दोनों होते हैं। क्या इसका यह अर्थ है कि कोई राशि जिसका परिमाण व दिशा हो, वह अवश्य ही सदिश होगी? किसी वस्तु के घूर्णन की व्याख्या घूर्णन-अक्ष की दिशा और अक्ष के परितः घूर्णन-कोण द्वारा की जा सकती है। क्या इसका यह अर्थ है कि कोई भी घूर्णन एक सदिश है?
