Question

कणों के किसी निकाय की गति को इसके द्रव्यमान केन्द्र की गति और द्रव्यमान केन्द्र के परितः गति में अलग-अलग करके विचार करना। दर्शाइए कि –

1.  `"p" = "p"_"i"^"'" + "m"_"i""V"` जहाँ है  `"p"_"i"` (m_i द्रव्यमान वाले) i-वे कण का संवेग है और `"p"_"i"^"'" = "m"_"i""v"_"i"^"'"`।  ध्यान दें कि `"v"_"i"^"'"` द्रव्यमान केन्द्र के सापेक्ष i – वे कण का वेग है। द्रव्यमान केन्द्र की परिभाषा का उपयोग करके यह भी सिद्ध कीजिए कि `∑"p"_"t"^"'" = "O"`
2. `"K" = "K"^"'" + 1//2 "MV"^2` K कणों के निकाय की कुल गतिज ऊर्जा, K’ = निकाय की कुल गतिज ऊर्जा जबकि कणों की गतिज ऊर्जा द्रव्यमान केन्द्र के सापेक्ष ली जाए। MV²/2 सम्पूर्ण निकाय के (अर्थात् निकाय के द्रव्यमान केन्द्र के) स्थानान्तरण की गतिज ऊर्जा है।
3. `"L" = "L"^"'" + "R" xx "MV"`
   जहाँ `"L"^"'" = ∑"r"_"i"^"'" = "r"_"i" - "R"` : शेष सभी चिह्न अध्याय में प्रयुक्त विभिन्न राशियों के मानक चिह्न हैं। ध्यान दें कि `"L"^"'"` द्रव्यमान केन्द्र के परितः निकाय का कोणीय संवेग एवं MR × V इसके द्रव्यमान केन्द्र का कोणीय संवेग है।
4. `"dL"^"'"/"dt" = ∑"r"_"i"^"'" xx "dp"^"'"/"dt"`
    यह भी दर्शाइए की `"dL"^"'"/"dt" = τ_"ext"^"'"`
   (जहाँ `τ_"ext"^"'"`द्रव्यमान केन्द्र के परितः निकाय पर लगने वाले सभी बाह्य बल आघूर्ण हैं।)
   [संकेत – दव्यमान केन्द की परिभाषा एवं न्यूटन के गति के तृतीय नियम का उपयोग कीजिए। यह मान लीजिए कि किन्ही दो कणों के बीच के आन्तरिक बल उनको मिलाने वाली रेखा के अनुदिश कार्य करते हैं।] 

Answer 1

(a) माना एक दॄढ पिण्ड n कणों से मिलकर बना है जिनके द्रव्यमान क्रमशः m₁. m₂, ........, m_n है तथा मुलबिन्दु O के सापेक्ष इन कणों के स्थिति सदिश क्रमशः `vec"r"_1,  vec"r"_2, ......, vec"r"_"i", .....vec"r"_"n"` है।

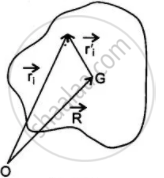
माना मूलबिंदु के सापेक्ष पिंड के द्रव्यमान केंद्र G का स्थिति सदिश `vec"R"` है तथा द्रव्यमान केंद्र के सापेक्ष अलग अलग कणों की स्थिति क्रमशः `vec"r"_1,  vec"r"_2, vec"r"_"i", .....vec"r"_"n"` है।

तब `vec"r"_"i" = vec"R" + vec"r"_"i"`

⇒ `"m"_"i"vec"r"_"i" = "m"_"i"vec"R" + "m"_"i"vec"r"_"i"`

t के सापेक्ष अवकलन करने पर,

`"m"_"i" ("d"vec"r"_"i")/"dt" = "m"_"i" ("d"vec"R")/"dt" + "m"_"i" ("d"vec"r"_"i")/"dt"`    ...(1)

परन्तु `"m"_"i" ("d"vec"r"_"i")/"dt" = "m"_"i" vec"v"_"i" = "i"` वें कण का मुलबिन्दु के सापेक्ष रेखीय संवेग = `vec"p"_"i"`

तथा `"m"_"i" ("d"vec"R")/"dt" = "m"_"i"   vec"V"` जहाँ  `vec"V"` = द्रव्यमान केंद्र का वेग है।

तथा `"m"_"i" ("d"vec"r"_"i")/"dt" = "m"_"i" vec"V"_"i" = vec"p"_"i" = "i"` वें कण का द्रव्यमान केंद्र क सापेक्ष रैखिक संवेग है।

∴ समीकरण (1) से,

`vec"p"_"i" = "m"_"i" vec"V" + vec"p"_"i"`    ...(2)

∵ द्रव्यमान केंद्र के परितः कणों के आघूर्णों का सदिश योग शून्य होता है; अतः

`Σ "m"_"i" vec"r"_"i" = vec"0"`

समय t के सापेक्ष दोनों पक्षों का अवकलन करने पर,

`∑"m"_"i" ("d"vec"r"_"i")/"dt"  = vec0`  या  `∑"m"_"i" vec"v"_"i" = vec 0`

 या `∑vec"p"_"i" = vec 0`

(b) ∵ `vec"r"_"i" = vec"R" + vec"r"_"i" => vec"dr"_"i"/"dt" = ("d"vec"R")/"dt"  + ("d"vec"r"_"i")/"dt"`

 या `vec"v"_"i" = "V" + vec"V"_"i"`

∴ `"v"_"i"^2 = vec"v"_"i" . vec"v"_"i" = (vec"V" + vec"V"_"i") . (vec"V" + vec"V"_"i")`

= `vec"V" . vec"V" + 2  vec "V" . vec"V"_"i" + vec"V"_"i" . vec"V"_"i" = "V"^2 + 2vec"V" . vec"V"_"i" + "V"_"i"^2`

∴ i वे कण की गतिज ऊर्जा

`"K"_"i" = 1/2 "m"_"i""v"_"i"^2=1/2"m"_"i""V"^2 + "m"_"i" vec"V" . vec"V"_"i" + 1/2 "m"_"i" "V"_1^2`

संपूर्ण पिंड की गतिज ऊर्जा 

`"K" = ∑"K"_"i" = ∑(1/2"m"_"i""V"^2 + "m"_"i" vec"V" . vec"V"_"i" + 1/2 "m"_"i" "V"_1^2)`

= `1/2 "V"^2 ∑"m"_"i"  +vec"V" . ∑"m"_"i" vec"V"_"i" + ∑1/2"m"_"i""V"_"i"^2`

= `1/2 "MV"^2 + vec"V" . ∑"p"_"i" + "K"^'`

जहाँ `∑"m"_"i" = "M"` पुरे पिंड का द्रव्यमान है तथा `∑1/2"m"_"i""V"_"i"^2`, द्रव्यमान केंद्र के सापेक्ष पुरे पिण्ड की गतिज ऊर्जा (घूर्णी) है तथा `1/2 "MV"^2` द्रव्यमान केंद्र की स्थानान्तरित गतिज ऊर्जा है।

∵ `∑vec"p"_"i" = vec0`

पुरे पिण्ड की गतिज ऊर्जा

`"K" = 1/2 "MV"^2 + "K"^"'"`

(c) समीकरण (2) में बाईं ओर से `vec"r"_"i"` का वेक्टर गुणन करने पर,

`vec"r"_"i" xx vec"p"_"i" = vec"r"_"i" xx ["m"_"i"vec"V" + "m"_"i"vec"V"_"i"]`

या `vec"L"_"i" = (vec"R" + vec"r"_"i") xx ["m"_"i" vec"V" + "m"_"i" vec"V"_"i"]`

= `vec"R" xx "m"_"i"vec"V" + vec"R" xx "m"_"i" vec"V"_"i" + vec"r"_"i" xx "m"_"i"vec"V" + vec"r"_"i" xx "m"_"i" vec"V"_"i"`

इस समीकरण का सभी कणों के लिए योग करने पर,

`∑vec"L"_"i" = ∑vec"R" xx "m"_"i"vec"V" + ∑vec"R" xx "m"_"i"vec"V"_"i" + ∑vec"r"_"i" xx "m"_"i"vec"V"_"i"`

या `vec"L" = vec"R" xx (∑"m"_"i") vec"V" + vec"R" xx (∑"m"_"i"vec"V"_"i") + (∑"m"_"i"vec"r"_"i") xx vec"V" + ∑vec"r"_"i" xx vec"p"_"i"`

= `vec"R" xx "M"vec"V" + vec"R" xx ∑ vec"P"_"i" + ∑"r"_"i" xx vec"p"_"i"`   `[∵ ∑ "m"_"i" vec"r"_"i" = vec0]` 

या `vec"L" = "R" xx "M"vec"V" + ∑vec"r"_"i" xx vec"p"_"i"`  `[∵ ∑vec"P"_"i" = vec0]`

या  `vec"L" = vec"R" xx "M"vec"V" + vec"L"`

यहाँ `vec"L"` संपूर्ण पिण्ड का मूलबिंदु के परितः कोणीय संवेग है तथा `vec"R" xx "M"vec"V"`, द्रव्यमान केंद्र का मूलबिंदु के सापेक्ष कोणीय संवेग है तथा `∑vec"r"_"i" xx vec"p"_"i" = vec"L"` पिण्ड का द्रव्यमान केंद्र के सापेक्ष कोणीय संवेग है।

(d) पुनः ∵ `vec"L" = ∑vec"r"_"i" xx vec"p"_"i"`

∴ समय t के सापेक्ष अवकलन करने पर,

`("d"vec"L")/"dt" = ∑(("d"vec"r"_"i")/"dt" xx vec"p"_"i" + vec"r"_"i" xx ("d"vec"p"_"i")/"dt")`

या `("d"vec"L")/"dt" = ∑vec"r"_"i" xx ("d"vec"p"_"i")/"dt"` [∵ `vec"V"_"i" xx "m"_"i" vec"V"_"i" = "m"_"i" (vec"V"_"i" xx vec"V"_"i") = vec0`]

अथवा `("d"vec"L")/"dt" = ∑vec"r"_"i" xx vec"F"_"i"`

यहाँ `("d"vec"p"_"i")/"dt" = vec"F"_"i"`,  i वे कण पर कार्यरत नेट बल है।

माना इस कण पर अन्य कणों के द्वारा आतंरिक आरोपित बलों का परिणामी `vec"F"_"i (internal)"` है तथा बाह्य आरोपित बल `vec"F"_"i (external)"` है तब

`vec"F"_"i" = vec"F"_"i (internal)" + vec"F"_"i (external)"`

तब `("d"vec"L")/"dt" = ∑vec"r"_"i" xx vec"F"_"i (internal)" + ∑vec"r"_"i" xx vec"F"_"i (external)"`

परन्तु सभी कणों पर आरोपित आंतरिक क्रिया - प्रतिक्रिया बल संतुलन में होते है तथा द्रव्यमान केंद्र के परितः इन बलों के आघुर्णों का सदिश योग शून्य होता है।

अर्थात `∑vec"r"_"i" xx vec"F"_"i  (internal)" = vec0`

जबकि `∑vec"r"_"i" xx vec"F"_"i  (external)" = vec"τ"_"ext"`

जहाँ `vec"τ"_"ext"`  पिण्ड पर आरोपित बाह्य बल का द्रव्यमान केंद्र के परितः आघूर्ण है।

अतः `("d"vec"L")/"dt" = vec"τ"_"ext"`