Advertisements
Advertisements
प्रश्न
Let there be n resistors R1............Rn with Rmax = max (R1......... Rn) and Rmin = min {R1..... Rn}. Show that when they are connected in parallel, the resultant resistance RP < R min and when they are connected in series, the resultant resistance RS > Rmax. Interpret the result physically.
उत्तर
Parallel grouping: Same potential difference appeared across each resistance but current distributes in the reverse ratio of their resistance, i.e. `i oo 1/R`
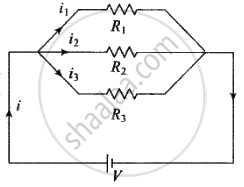
Series grouping: Same current flows through each resistance but potential difference distributes in the ratio of resistance, i.e. `V oo R`
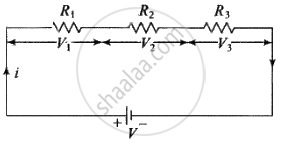
In parallel combination: When all resistances are connected in parallel, the equivalent resistance Rρ is given by
`1/R_ρ = 1/R_1 + ... + 1/R_n`
By multiplying both sides by Rmin, we have
`R_(min)/R_ρ = R_(min)/R_1 + R_(min)/R_2 + ... + R_(min)/R_n`
Here, in RHS, there exists one term `R_(min)/R_(min)` = 1 and other terms are positive, so we have
`R_(min)/R_ρ = R_(min)/R_1 + R_(min)/R_2 + ... + R_(min)/R_n > 1`
This shows that the resultant resistance Rρ < Rmin.
Thus, in parallel combination, the equivalent resistance of resistors is even less than the minimum resistance available in a combination of resistors.
In series combination: When all resistances are connected in series, the equivalent resistance Rs is given by
Rs = R1 + ... + Rn
Here, in RHS, there exist one term having resistance Rmax.
So, we have
or Rs = R1 + ... + Rmax ... + ... + Rn
Rs = R1 + ... + Rmax ... + Rn = Rmax + ... (R1 + ... + )Rn
or Rs ≥ Rmax
Rs = Rmax(R1 + ... + Rn)
Thus, in series combination, the equivalent resistance of resistors is greater than the maximum resistance available in a combination of resistors.
Physical interpretation:
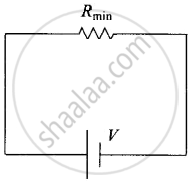 (a) |
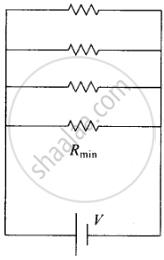 (b) |
In figure (b), Rmin provides an equivalent routine as in figure. (a) for current. But in addition, there are (n – 1) routes by the remaining (n – 1) resistors. Current in figure. (b) is greater than current in figure (a) Effective resistance in figure. (b) < Rmin. Second circuit evidently affords a greater resistance.
 (c) |
 (d) |
In figure (d), Rmax provides an equivalent route as in figure. (c) for current. Current in figure (d) < current in figure (c). Effective resistance in figure. (d) > Rmax. Second circuit evidently affords a greater resistance.
APPEARS IN
संबंधित प्रश्न
Three resistors 2 Ω, 4 Ω and 5 Ω are combined in parallel. What is the total resistance of the combination?
Two heating elements of resistances R1 and R2 when operated at a constant supply of voltage, V, consume powers P1 and P2 respectively. Deduce the expressions for the power of their combination whey they are, in turn, connected in (i) series and (ii) parallel across the same voltage supply.
A bulb is made using two filaments. A switch selects whether the filaments are used individually or in parallel. When used with a 15 V battery, the bulb can be operated at 5 W, 10 W or 15 W. What should be the resistances of the filaments?
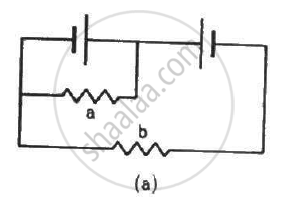
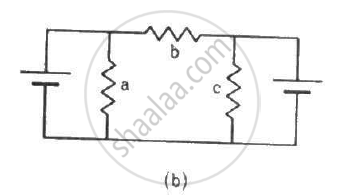
Each of the resistors shown in the figure has a resistance of 10 Ω and each of the batteries has an emf of 10 V. Find the currents flowing through the resistors a and bin the two circuits.
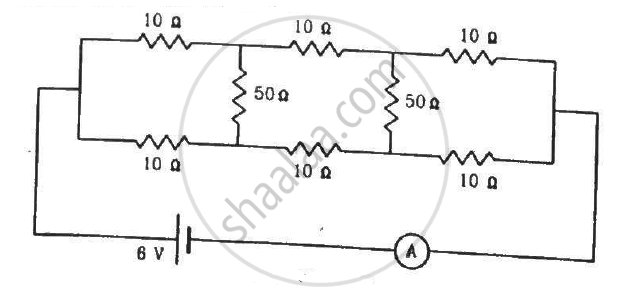
Find the current measured by the ammeter in the circuit shown in the figure.
A voltmeter coil has resistance 50.0 Ω and a resistor of 1.15 kΩ is connected in series. It can read potential differences up to 12 volts. If this same coil is used to construct an ammeter that can measure currents up to 2.0 A, what should be the resistance of the shunt used?
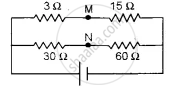
How much resistance should be connected to 15 Ω resistor shown in the circuit in figure below so that the points M and N are at the same potential:
An ammeter together with an unknown resistance in series is connected across two identical batteries each of emf 1.5 V. When the batteries are connected in series, the galvanometer records a current of 1A and when the batteries are in parallel, the current is 0.6A. Then the internal resistance of the battery is ______.
