Advertisements
Advertisements
Question
Let there be n resistors R1............Rn with Rmax = max (R1......... Rn) and Rmin = min {R1..... Rn}. Show that when they are connected in parallel, the resultant resistance RP < R min and when they are connected in series, the resultant resistance RS > Rmax. Interpret the result physically.
Solution
Parallel grouping: Same potential difference appeared across each resistance but current distributes in the reverse ratio of their resistance, i.e. `i oo 1/R`
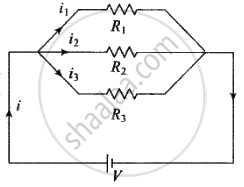
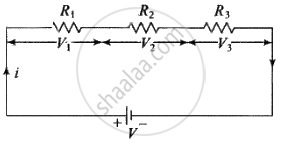
Series grouping: Same current flows through each resistance but potential difference distributes in the ratio of resistance, i.e. `V oo R`
In parallel combination: When all resistances are connected in parallel, the equivalent resistance Rρ is given by
`1/R_ρ = 1/R_1 + ... + 1/R_n`
By multiplying both sides by Rmin, we have
`R_(min)/R_ρ = R_(min)/R_1 + R_(min)/R_2 + ... + R_(min)/R_n`
Here, in RHS, there exists one term `R_(min)/R_(min)` = 1 and other terms are positive, so we have
`R_(min)/R_ρ = R_(min)/R_1 + R_(min)/R_2 + ... + R_(min)/R_n > 1`
This shows that the resultant resistance Rρ < Rmin.
Thus, in parallel combination, the equivalent resistance of resistors is even less than the minimum resistance available in a combination of resistors.
In series combination: When all resistances are connected in series, the equivalent resistance Rs is given by
Rs = R1 + ... + Rn
Here, in RHS, there exist one term having resistance Rmax.
So, we have
or Rs = R1 + ... + Rmax ... + ... + Rn
Rs = R1 + ... + Rmax ... + Rn = Rmax + ... (R1 + ... + )Rn
or Rs ≥ Rmax
Rs = Rmax(R1 + ... + Rn)
Thus, in series combination, the equivalent resistance of resistors is greater than the maximum resistance available in a combination of resistors.
Physical interpretation:
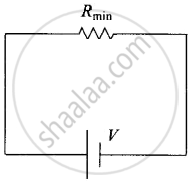 (a) |
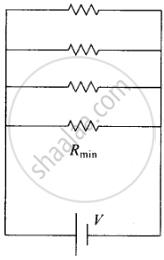 (b) |
In figure (b), Rmin provides an equivalent routine as in figure. (a) for current. But in addition, there are (n – 1) routes by the remaining (n – 1) resistors. Current in figure. (b) is greater than current in figure (a) Effective resistance in figure. (b) < Rmin. Second circuit evidently affords a greater resistance.
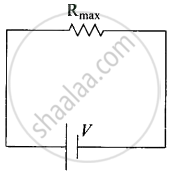 (c) |
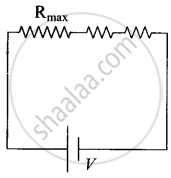 (d) |
In figure (d), Rmax provides an equivalent route as in figure. (c) for current. Current in figure (d) < current in figure (c). Effective resistance in figure. (d) > Rmax. Second circuit evidently affords a greater resistance.
APPEARS IN
RELATED QUESTIONS
Three identical cells each of emf 2V and internal resistance 10 Ω are connected in series to form a battery. The battery is then connected to a parallel combination of two identical resistors, each of resistance 6 Ω. Find the current delivered by the battery.
Suppose you have three resistors of 20 Ω, 50 Ω and 100 Ω. What minimum and maximum resistance can you obtain from these resistors?
A bulb is made using two filaments. A switch selects whether the filaments are used individually or in parallel. When used with a 15 V battery, the bulb can be operated at 5 W, 10 W or 15 W. What should be the resistances of the filaments?
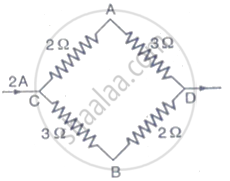
A current of 2 A flows in conductors as shown. The potential difference VA- VB will be ________.
The instantaneous values of emf and the current in a series ac circuit are-
E = Eo Sin ωt and I = Io sin (ωt+π/3) respectively, then it is ______.
How many times will the resistance of an identical conductor be increase, if the parallel resistance be change to series one?
A condenses having a capacity 2.0 µF is charged to 200 V and the plates of the capacitor are connected to a resistance wire. The heat produce in it will be:-
The effective resistance of a parallel connection that consists of four wires of equal length, equal area of cross-section and the same material is 0.25 Ω. What will be the effective resistance if they are connected in series?
