Advertisements
Advertisements
प्रश्न
Light waves each of amplitude "a" and frequency "ω", emanating from two coherent light sources superpose at a point. If the displacements due to these waves are given by y1 = a cos ωt and y2 = a cos(ωt + ϕ) where ϕ is the phase difference between the two, obtain the expression for the resultant intensity at the point.
उत्तर
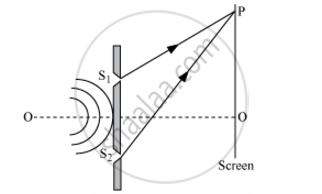
Let the displacement of the waves from the sources S1 and S2 at point P on the screen at any time t be given by:
y1 = a cos ωt
and
y2 = a cos (ωt + Φ)
where, Φ is the constant phase difference between the two waves
By the superposition principle, the resultant displacement at point P is given by:
y = y1 + y2
y = a cos ωt + a cos (ωt + Φ)
`=2a[cos((omegat+omegat+phi)/2)cos((omegat-omegat-phi)/2)]`
`y=2acos(omegat+phi/2)cos(phi/2)" ...(i)"`
Let 2 `acos(phi/2)=A ...(ii)"`
Then, equation (i) becomes:
`y=Acos(omegat+phi/2)`
Now, we have:
`A^2=4a^2cos^2(phi/2)" ..(iii)"`
The intensity of light is directly proportional to the square of the amplitude of the wave. The intensity of light at point P on the screen is given by:
`I=4a^2cos^2(phi/2)" ...(iv)"`
APPEARS IN
संबंधित प्रश्न
Two wave pulses identical in shape but inverted with respect to each other are produced at the two ends of a stretched string. At an instant when the pulses reach the middle, the string becomes completely straight. What happens to the energy of the two pulses?
A tuning fork of frequency 480 Hz is used to vibrate a sonometer wire having natural frequency 410 Hz. The wire will vibrate with a frequency
A 4⋅0 kg block is suspended from the ceiling of an elevator through a string having a linear mass density of \[19 \cdot 2 \times {10}^{- 3} kg m^{- 1}\] . Find the speed (with respect to the string) with which a wave pulse can proceed on the string if the elevator accelerates up at the rate of 2⋅0 m s−2. Take g = 10 m s−2.
Two waves, each having a frequency of 100 Hz and a wavelength of 2⋅0 cm, are travelling in the same direction on a string. What is the phase difference between the waves (a) if the second wave was produced 0⋅015 s later than the first one at the same place, (b) if the two waves were produced at the same instant but first one was produced a distance 4⋅0 cm behind the second one? (c) If each of the waves has an amplitude of 2⋅0 mm, what would be the amplitudes of the resultant waves in part (a) and (b) ?
Answer briefly.
State and explain the principle of superposition of waves.
If `sqrt("A"^2+"B"^2)` represents the magnitude of resultant of two vectors `(vec"A" + vec"B")` and `(vec"A" - vec"B")`, then the angle between two vectors is ______.
The wavelength of light used in young.'s double slit experiment is λ. The intensity at a point on the screen is I where the path difference is λ/6. If I0 denotes the maximum intensity, then the ratio of I and I0 is ______.
Consider a ray of light incident from air onto a slab of glass (refractive index n) of width d, at an angle θ. The phase difference between the ray reflected by the top surface of the glass and the bottom surface is ______.
For the harmonic travelling wave y = 2 cos 2π (10t – 0.0080x + 3.5) where x and y are in cm and t is second. What is the phase difference between the oscillatory motion at two points separated by a distance of 0.5 m
For the harmonic travelling wave y = 2 cos 2π (10t – 0.0080x + 3.5) where x and y are in cm and t is second. What is the phase difference between the oscillatory motion at two points separated by a distance of What is the phase difference between the oscillation of a particle located at x = 100 cm, at t = T s and t = 5 s?
