Advertisements
Advertisements
प्रश्न
ΔMNT ~ ΔQRS, बिंदु T से खींचे गए शीर्षलंब की लंबाई 5 तथा बिंदु S से खींचे गए शीर्षलंब की लंबाई 9 है, तो `("A"(Δ"MNT"))/("A"(Δ"QRS"))` यह अनुपात ज्ञात कीजिए।
उत्तर
माना, ΔMNT में शीर्षबिंदु T से खींचा गया शीर्षलंब TX और ΔQRS में शीर्षबिंदु S से खींचा गया शीर्षलंब SY इस प्रकार है कि , M-X-N और R-Y-Q.
TX = 5 और SY = 9.
∵ ΔMNT ∼ ΔQRS .........(दत्त)
∴ ∠M ≅ ∠Q .........(समरूप त्रिभुजों के संगत कोण) ....(1)
ΔMXT और ΔQYS में,
∠XMT ≅ ∠YQS .....[(1) से]
∠MXT ≅ ∠QYS ......(प्रत्येक 90°)
∴ ΔMXT ∼ ΔQYS ......(समरूपता की को-को कसौटी)
∴ `"TM"/"SQ" = "TX"/"SY"` ....(समरूप त्रिभुजों की संगत भुजाएँ समानुपात होती है)
∴ `"TM"/"SQ" = 5/9` ..........(2)
ΔMNT ∼ ΔQRS .................(दत्त)
`("A"(Δ"MNT"))/("A"(Δ"QRS")) = "TM"^2/"SQ"^2` .....(समरूप त्रिभुजों के क्षेत्रफलों का प्रमेय)
∴ `("A"(Δ"MNT"))/("A"(Δ"QRS")) = ("TM"/"SQ")^2`
∴ `("A"(Δ"MNT"))/("A"(Δ"QRS")) = (5/9)^2 = 25/81`
∴ `("A"(Δ"MNT"))/("A"(Δ"QRS")) = underline(25/81)` है |
APPEARS IN
संबंधित प्रश्न
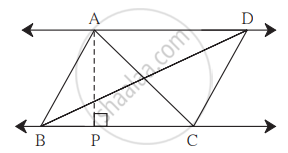
संलग्न आकृति में AP ⊥ BC, AD || BC, तो A(ΔABC) : A(ΔBCD) का मान ज्ञात कीजिए।
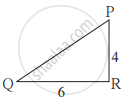
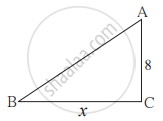
आकृति में दर्शाएअनुसार 8 मीटर तथा 4 मीटर ऊँचाईवाले दो खंभे समतल जमीन पर खड़े हैं। सूर्य के प्रकाश से छोटे खंभे की परछाई 6 मीटर होती हो तो उसी समय बड़े खंभे की परछाईं की लंबाई कितनी होगी?
ΔABC ~ ΔPQR, A(ΔABC) = 80, A(ΔPQR) = 125 तो निम्नलिखित रिक्त चौखटों को पूरा कीजिए।
`("A"(Δ"ABC"))/("A"(Δsquare)) = 80/125 = square/square`
∴ `"AB"/"PQ" = square/square`
ΔLMN ~ ΔPQR, 9 × A(ΔPQR ) = 16 × A (ΔLMN), यदि QR = 20 तो MN का मान ज्ञात कीजिए।
निम्नलिखित उपप्रश्न के पर्यायी उत्तर दिए गए हैं। इनमें से सही पर्याय चुनिए।
ΔABC तथा ΔDEF में ∠B = ∠E, ∠F = ∠C और AB = 3 DE, तो इन दोनों त्रिभुजों के लिए कौन-सा कथन सत्य है?
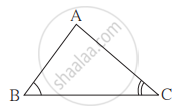

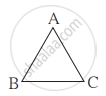
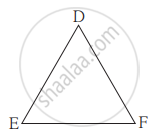
समबाहु ΔABC तथा ΔDEF में, A(ΔABC) : A(ΔDEF) = 1 : 2 होने पर AB = 4 हो तो DE की लंबाई कितनी?
ΔABC में B – D – C और BD = 7, BC = 20, तो निम्नलिखित अनुपात ज्ञात कीजिए।
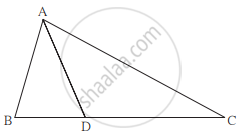
`(A(∆ABD))/(A(∆ABC))`
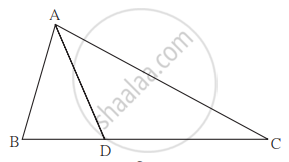
ΔABC में B - D – C और BD = 7, BC = 20 तो निम्नलिखित अनुपात ज्ञात कीजिए।
`("A"(Δ"ADC"))/("A"(Δ"ABC"))`
ΔABC में रेख DE || भुजा BC | यदि 2A(ΔADE) = A(⬜ DBCE), तो AB : AD का मान ज्ञात कीजिए तथा सिद्ध कीजिए BC = `sqrt3` DE |
यदि Δ ABC और ~ Δ PQR और AB : PQ = 2 : 3 तो `(A(Δ "ABC"))/(A(Δ "PQR")` का मान ज्ञात कीजिए।
