Advertisements
Advertisements
प्रश्न
Mr. Rajesh. Has Rs. 1800 to spend on fruits for a meeting. Grapes cost Rs. 150 per kg. and peaches cost Rs. 200 per kg. Formulate and solve it graphically.
उत्तर
The cost of grapes = Rs. 150/- per kg.
Let x kg of grapes be bought.
Then total cost of grapes = 150 x
The cost of peaches = Rs.200/- per kg.
Let y kg of peaches be bought.
Then total cost of peaches = 200 y
Since Mr. Rajesh has total amount Rs. 1800 to spend on fruits.
His total expenses 150 x + 200 y should be less than or equal to 1800.
Inequation is 150x + 200y ≤ 1800
⇒ 3x + 4y ≤ 36 ......(i)
x, y ≥ 0 as the quantities of grapes and peaches can’t be negative.
Points on axes are
| x | 12 | 0 |
| y | 0 | 9 |
(12, 0) on X-axis and (0, 9) on Y-axis.
Since origin satisfies the inequation, solution set is towards origin.
Since x and y are both positive, the solution lies in the first quadrant only.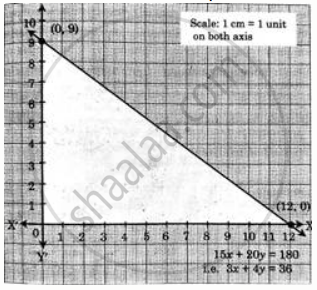
APPEARS IN
संबंधित प्रश्न
Solve the inequation:
`("x" - 2)/("x" + 5) > 0`
Solve the following inequation graphically in the two-dimensional plane.
y ≥ 3
Solve the following inequations graphically in two-dimensional plane.
y ≤ – 2x
Solve the following inequation graphically in the two-dimensional plane.
x – y ≥ 0
Solve the following inequation graphically in two-dimensional plane.
2x – y ≤ − 2
Solve the following inequation graphically in the two-dimensional plane.
4x + 5y ≤ 40
Solve the following inequation graphically in the two-dimensional plane.
`1/4 "x" + 1/2 "y" ≤ 1`
Diet of a sick person must contain at least 4000 units of vitamin. Each unit of food F1 contains 200 units of vitamin, where as each unit of food F2 contains 100 units of vitamins. Write an inequation to fulfil sick person’s requirements and represent the solution set graphically.
Find the graphical solution of the following system of linear inequations:
3x + 2y ≤ 24, 3x + y ≥ 15, x ≥ 4
Solve the following system of inequalities graphically.
x + y ≥ 4, 2x – y ≤ 0
Solve the following system of inequalities graphically.
x + y ≤ 6, x + y ≥ 4
Solve the following system of inequalities graphically.
2x + y ≥ 8, x + 2y ≥ 10
Solve the following system of inequalities graphically.
3x + 4y ≤ 60, x + 3y ≤ 30, x ≥ 0, y ≥ 0
Solve the following system of inequalities graphically.
x – 2y ≤ 3, 3x + 4y ≥ 12, x ≥ 0, y ≥ 1
Solve the following system of inequalities graphically.
4x + 3y ≤ 60, y ≥ 2x, x ≥ 3, x, y ≥ 0
Find the graphical solution of the following system of linear inequations:
0 ≤ x ≤ 350, 0 ≤ y ≤ 150
