Advertisements
Advertisements
प्रश्न
Solve the following inequation graphically in the two-dimensional plane.
`1/4 "x" + 1/2 "y" ≤ 1`
उत्तर
Given, inequation is `1/4 "x" + 1/2 "y" ≤ 1`
∴ corresponding equation is `"x"/4+"y"/2=1`
The two points required to plotting the line on the graph are
| x | 4 | 0 |
| y | 0 | 2 |
(4, 0) and (0, 2) on the X and Y are respectively.
Substitute x = 0, y = 0 in the inequation.
`1/4(0)+1/2(0)≤1`
i.e. 0 ≤ 1.
Origin satisfies the inequation on showing that the solution set contains the origin.
The solution set is towards the origin.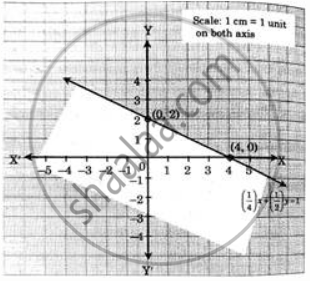
APPEARS IN
संबंधित प्रश्न
Solve the following inequation graphically in the two-dimensional plane.
y ≥ 3
Solve the following inequations graphically in two-dimensional plane.
y ≤ – 2x
Solve the following inequation graphically in the two-dimensional plane.
y – 5x ≥ 0
Solve the following inequation graphically in the two-dimensional plane.
x – y ≥ 0
Solve the following inequation graphically in two-dimensional plane.
2x – y ≤ − 2
Mr. Rajesh. Has Rs. 1800 to spend on fruits for a meeting. Grapes cost Rs. 150 per kg. and peaches cost Rs. 200 per kg. Formulate and solve it graphically.
Find the graphical solution of the following system of linear inequations:
3x + 2y ≤ 24, 3x + y ≥ 15, x ≥ 4
Find the graphical solution of the following system of linear inequations:
2x + y ≥ 8, x + 2y ≥ 10, x ≥ 0, y ≥ 0
Solve the following system of inequalities graphically.
2x + y ≥ 6, 3x + 4y ≤ 12
Solve the following system of inequalities graphically.
2x + y ≥ 8, x + 2y ≥ 10
Solve the following system of inequalities graphically.
x + y ≤ 9, y > x, x ≥ 0
Solve the following system of inequalities graphically.
5x + 4y ≤ 20, x ≥ 1, y ≥ 2
Solve the following system of inequalities graphically.
3x + 4y ≤ 60, x + 3y ≤ 30, x ≥ 0, y ≥ 0
Solve the following system of inequalities graphically.
x – 2y ≤ 3, 3x + 4y ≥ 12, x ≥ 0, y ≥ 1
Solve the following system of inequalities graphically.
4x + 3y ≤ 60, y ≥ 2x, x ≥ 3, x, y ≥ 0
Find the graphical solution of the following system of linear inequations:
0 ≤ x ≤ 350, 0 ≤ y ≤ 150
