Advertisements
Advertisements
प्रश्न
मृदु इस्पात के एक तार, जिसकी लंबाई 1.0 m तथा अनुप्रस्थ परिच्छेद का क्षेत्रफल – 0.50 x 10-2 cm2 है, को दो खम्भों के बीच क्षैतिज दिशा में प्रत्यास्थ सीमा के अन्दर ही तनित किया जाता है। तार के मध्य बिन्दु से 100g का एक द्रव्यमान लटका दिया जाता है। मध्य बिन्दु पर अवनमन की गणना कीजिए।
उत्तर
दिया है : तार की लंबाई L = 1.0 m,
अनुप्रस्थ परिच्छेद का क्षेत्रफल A = 0.50 x 10-2 cm2 = 5 x 10-7 m2
m = 100 g = 0.1 kg, Y = 2.0 x 1011 Nm-2
माना सन्तुलन की स्थिति में तार के दोनों भागों का क्षैतिज से – झुकाव θ है तथा तार के दोनों भागों में समान तनाव T है।
सन्तुलन की स्थिति में,
2T sin θ = mg …(1)
(C तार का मध्य बिन्दु है जो भार लटकाने पर बिन्दु O तक विस्थापित हो जाता है।)
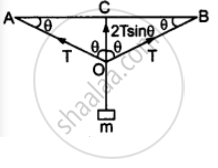
तब `"l" = "AC" = "BC" = 1.0/2 = 0.5` m
माना अवनमन OC = x है जो की सूक्ष्म होगा।
∴ AO = `sqrt("AC"^2 + "OC"^2) = sqrt("l"^2 + x^2)`
∴ भाग AC की लंबाई में वृद्धि `triangle"l" = "AO" - "AC"`
= `("l"^2 + x^2)^(1//2) - "l"`
= `"l"[(1 + x^2/"l"^2)^(1//2) - 1]`
`triangle"l" = "l"[(1 + 1/2 x^2/"l"^2) - 1]` (द्विपद प्रमेय से)
अथवा `triangle"l" = "l" xx x^2/(2"l"^2)`
∴ भाग AO में तनाव `"T" = ("YA"triangle"l")/"l"` ` [∵ "Y" = ("T"//"A")/(triangle"l"//"l")]`
= `"YA"/"l" xx "l" xx x^2/(2"l"^2) = ("YA"x^2)/(2"l"^2)`
∴ समीकरण (1) से `2 xx ("YA"x^2)/(2"l"^2)` sin θ = mg
`=> "sin" theta = ("mg" "l"^2)/"YA"` परन्तु θ छोटा है ` => "sin"theta = theta = "OC"/"AC" = x/"l"`
∴ `x/"l" = ("mg" "l"^2)/("YA"x^2) => x^3 = "mgl"^3/"YA"`
∴ `x = "l" xx ("mg"/"YA")^(1//3) = 0.5 "m"[(0.1 "kg" xx 9.8 "ms"^-2)/(2.0 xx 10^11 "N" "m"^-2 xx 5 xx 10^-7 "m"^2)]^(1/3)`
`= 0.5 xx 2.13 xx 10^-2 "m" ≈ = 0.01` m
अतः मध्य बिन्दु पर अवनमन लगभग 0. 01 m है।
APPEARS IN
संबंधित प्रश्न
मृदु इस्पात के चार समरूप खोखले बेलनाकार स्तम्भ 50,000 kg द्रव्यमान के किसी बड़े ढाँचे को आधार दिए हुए हैं। प्रत्येक स्तम्भ की भीतरी तथा बाहरी त्रिज्याएँ क्रमशः 30 तथा 60 cm हैं। भार वितरण को एकसमान मानते हुए प्रत्येक स्तम्भ की संपीडन विकृति की गणना कीजिए।
1.5 cm त्रिज्या का एक इस्पात का केबिल भार उठाने के लिए इस्तेमाल किया जाता है। | यदि इस्पात के लिए अधिकतम अनुज्ञेय प्रतिबल 108 Nm-2 है तो उस अधिकतम भार की गणना कीजिए जिसे केबिल उठा सकता है।
15 kg द्रव्यमान की एक दृढ़ पट्टी को तीन तारों, जिनमें से प्रत्येक की लंबाई 2 m है, से सममित लटकाया गया है। सिरों के दोनों तार ताँबे के हैं तथा बीच वाली तार लोहे का है। तारों के व्यासों के अनुपात ज्ञात कीजिए जबकि प्रत्येक पर तनाव उतना ही रहता है।
ताँबे के एक ठोस धन का एक किनारा 10 cm का है। इस पर 7.0 × 106 Pa का जलीय दाब लगाने पर इसके आयतन में संकुचन निकालिए।
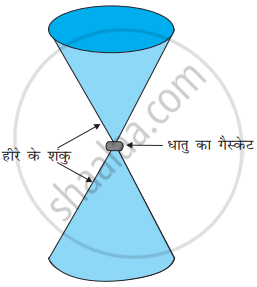
हीरे के एकल क्रिस्टलों से बनी निहाइयों, जिनकी आकृति चित्र में दिखाई गई है, का उपयोग अति उच्च दाब के अंतर्गत द्रव्यों के व्यवहार की जाँच के लिए किया जाता है। निहाई के संकीर्ण सिरों पर सपाट फलकों का व्यास 0.50 mm है। यदि निहाई के चौड़े सिरों पर 50,000 N का बल लगा हो तो उसकी नोंक पर दाब ज्ञात कीजिए।
धातु के दो पहियों के सिरों को चार रिवेट से आपस में जोड़ दिया जाता है। प्रत्येक रिवेट का व्यास 6 मिमी है। यदि रिवेट का अपरुपण प्रतिबल 6.9 x 107 Pa से अधिक नहीं बढ़ना | हो तो रिवेट की हुई पट्टी द्वारा आरोपित तनाव का अधिकतम मान कितना होगा? मान लीजिए कि प्रत्येक रिवेट एक-चौथाई भार वहन कर सकता है।
