Advertisements
Advertisements
प्रश्न
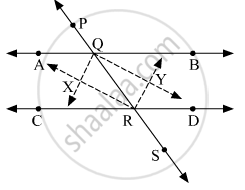
निचे दी गई आकृति के आधार पर रेखा AB || रेखा CD तथा रेखा PS उसकी तिर्यक रेखा है। किरण QX, किरण QY, किरण RX तथा किरण RY यह कोणों की समद्विभाजक है। तो सिद्ध कीजिए कि `square` QXRY एक आयत है।
उत्तर
दिया गया : AB और CD दो समानांतर रेखाएँ हैं जो एक तिर्यक छेदी PS द्वारा बिंदु Q और R पर प्रतिछेदित की जाती हैं।
क्रमश : आंतरिक कोणों के समद्विभाजक बिंदु X और Y पर प्रतिच्छेदित करते हैं।
सिद्ध : चतुर्भुज QXRY एक आयत है।
प्रमाण : चूँकि AB || CD और PS एक तिर्यक रेखा है,
∠AQR = ∠DRQ (अंतः कोण)
⇒ `1/2` ∠AQR = `1/2`∠DRQ ...(1)
चूँकि QX, ∠AQR को समद्विभाजित करता है और RY, ∠DRQ को समद्विभाजित करता है, तो
∠XQR = `1/2`∠AQR और ∠YRQ = `1/2`∠DRQ
∴ (1) से,
∠XQR = ∠YRQ
लेकिन ∠XQR और ∠YRQ एकांतर आंतरिक कोण हैं जो QX के साथ तिर्यक रेखा QR द्वारा बनते हैं और क्रमशः RY
∴ QX || RY ...(एकांतर कोण कसौटी )
इसी तरह, RX || QY.
इसलिए, चतुर्भुज QXRY में, हमारे पास QX || RY और RX || QY है।
यह ज्ञात है कि, एक चतुर्भुज एक समांतर चतुर्भुज होता है यदि इसकी सम्मुख भुजाएँ समांतर हों।
∴ QXRY एक समांतर चतुर्भुज है।
तथा तिर्यक रेखा के एक ही तरफ के आंतरिक कोणों का योग 180° है, तो
∠BQR + ∠DRQ = 180°
⇒`1/2`∠BQR + `1/2`∠DRQ = 90° ...(2)
अर्थात QY, ∠BQR को समद्विभाजित करता है और RY, ∠DRQ को समद्विभाजित करता है, तो
∠YQR = `1/2`∠BQR और ∠YRQ = `1/2`∠DRQ
∴ (2) से,
∠YQR + ∠YRQ = 90∘ ....(3)
∆QRY में, हमारे पास है
∠YQR + ∠YRQ + ∠QYR = 180∘ ...(त्रिभुज का कोण योग गुण)
⇒ 90∘ + ∠QYR = 180∘ ...[(3) का उपयोग करके]
⇒ ∠QYR = 180∘ − 90∘ = 90∘
तथा QXRY एक समांतर चतुर्भुज है, तो
∠QXR = ∠QYR ...(समांतर चतुर्भुज के सम्मुख कोण बराबर होते हैं)
⇒∠QXR = 90∘ ...(∵ ∠QYR = 90∘)
समांतर चतुर्भुज में सभी कोण संपूरक होते हैं, तो
∠QXR + ∠XRY = 180∘
⇒ 90∘ + ∠XRY = 180∘ ...(∵ ∠QXR = 90∘)
⇒ ∠XRY = 180∘ − 90∘
⇒ ∠XRY = 90∘
साथ ही, ∠XQY = ∠XRY = 90∘ ...(समांतर चतुर्भुज के सम्मुख कोण बराबर होते हैं)
इस प्रकार, QXRY एक समांतर चतुर्भुज है जिसके सभी आंतरिक कोण समकोण हैं।
यह ज्ञात है कि, एक आयत एक समांतर चतुर्भुज है जिसका प्रत्येक कोण एक समकोण होता है।
अतः, `square` QXRY एक आयत है।
APPEARS IN
संबंधित प्रश्न
आकृति में, y = 108° तथा x = 71° तो रेखा m तथा रेखा n समांतर होगी, कारण लिखिए।
निचे दी गई आकृति यदि ∠a ≅ ∠b तो सिद्ध कीजिए कि रेखा l || रेखा m

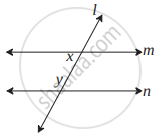
आकृति में यदि ∠a ≅ ∠b और ∠x ≅ ∠y तो सिद्ध कीजिए कि रेखा l || रेखा n

दो रेखाओं को किसी तिर्यक रेखा द्वारा प्रतिच्छेदित करने पर ______ कोण निर्मित होते हैं ।
ΔABC में ∠A = 76°, ∠B = 48°, तो ∠C का माप ______ है ।
दो समांतर रेखाओं को किसी तिर्यक रेखा द्वारा प्रतिच्छेदित करने पर बनने वाले एकांतर कोणों की जोड़ी में से यदि एक कोण का माप 75° हो तो दूसरे कोण का माप ______ होता है।
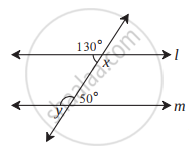
निचे दी गई आकृति में दिए गए कोणों के मापों के आधार पर ∠x तथा ∠y के माप ज्ञात करे। सिद्ध कीजिए कि रेखा l || रेखा m