Advertisements
Advertisements
प्रश्न
नीचे दी गयी आक़ति में, एक आयत MORE दर्शाया गया है –
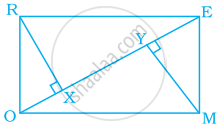
उचित कारण देते हुए, निम्न प्रश्नों के उत्तर दीजिए –
- क्या RE = OM है?
- क्या ∠MYO = ∠RXE है?
- क्या ∠MOY = ∠REX? है?
- क्या ∆MYO ≅ ∆RXE है?
- क्या MY = RX है?
उत्तर
i. हाँ, RE = OM
दिया गया है, MORE एक आयत है।
इसलिए, सम्मुख भुजाएँ बराबर होती हैं।
ii. हाँ, ∠MYO = ∠RXE
यहाँ, MY और RX, OE के लंबवत हैं।
चूँकि, ∠RXO = 90°
⇒ ∠RXE = 90° और ∠MYE = 90°
⇒ ∠MYO = 90°
iii. हाँ, ∠MOY = ∠REX
∵ RE || OM और EO एक तिर्यक रेखा है।
∴ ∠MOE = ∠OER ...[∵ वैकल्पिक आंतरिक कोण]
⇒ ∠MOY = ∠REX
iv. हाँ, ∆MYO ≅ ∆RXE
∆MYO और ∆RXE में
MO = RE ...[(i) में सिद्ध]
∠MOY = ∠REX ...[(iii) में सिद्ध किया गया]
∠MYO = ∠RXE ...[(ii) में सिद्ध किया गया]
∴ ∆MYO = ∆RXE ...[AAS द्वारा]
v. हाँ, MY = RX
चूँकि, ये सर्वांगसम त्रिभुजों के संगत भाग हैं।
APPEARS IN
संबंधित प्रश्न
बताइए एक आयत उत्तल चतुर्भुज कैसे है।
निम्नलिखित के लिए कारण दीजिए:
वर्ग को एक विशेष प्रकार का आयत समझा जा सकता है।
एक सम अष्टभुज (regular octagon) का एक रफ़ चित्र खींचिए। [यदि आप चाहें, तो वर्गांकित कागज़ (squared paper) का प्रयोग कर सकते हैं।] इस अष्टभुज के चार शीर्षों को जोड़कर एक आयत खींचिए।
एक चतुर्भुज जिसकी सम्मुख भुजाएँ और सभी कोण बराबर हों, होता है एक ______।
QR = 6 cm, PQ = 4 cm और ∠PQR = 90∘ के साथ एक समांतर चतुर्भुज की रचना की जाती है। तब PQRS है एक ______।
आयत एक सम चतुर्भुज है।
प्रत्येक आयत एक समलंब है।
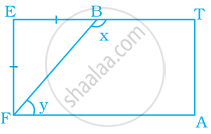
एक खेल का मैदान एक आयत ATEF के रूप का है। दो खिलाड़ी बिंदु F और B पर खड़ हैं, जहाँ EF = EB है। x और y के मान ज्ञात कीजिए।
रेखा l रेखा m के समांतर है तथा एक तिर्यक रेखा p क्रमशः इन्हें X और Y पर प्रतिच्छेद करती है। X और Y पर स्थित अंतःकोणों के समद्विभाजक P और Q प्रतिच्छेद करते हैं। क्या PXQY एक आयत है? कारण दीजिए।
एक आयत की रचना कीजिए, जिसकी एक भुजा 3 cm और विकर्ण 5 cm है।
