Advertisements
Advertisements
प्रश्न
निम्नलिखित पद की परिभाषा दीजिए। क्या इनके लिए कुछ ऐसे पद हैं, जिन्हें परिभाषित करने की आवश्यकता है? वे क्या हैं और आप इन्हें कैसे परिभाषित कर पाएँगे?
वर्ग
उत्तर
वर्ग एक चतुर्भुज होता है जिसकी सभी भुजाएँ समान लंबाई की होती हैं और सभी कोण एक ही माप के होते हैं, यानी 90°। वर्ग को परिभाषित करने के लिए, हमें चतुर्भुज, भुजा और कोण के बारे में जानना चाहिए।

APPEARS IN
संबंधित प्रश्न
आकृति में, यदि AC = BD है, तो सिद्ध कीजिए कि AB = CD है।

यूक्लिड के कथन, सभी समकोण एक दूसरे के बराबर होते हैं, निम्नलिखित के रूप में दिया गया है :
ठोसों की परिसीमाएँ वक्र होती हैं।
एक पृष्ठ के किनारे वक्र होते हैं।
कथन “प्रत्येक रेखा l और उस पर न स्थित प्रत्येक बिंदु P के लिए, एक अद्वितीय रेखा का अस्तित्व है जो P से होकर जाती है और l के समांतर है” प्लेफेयर अभिगृहीत कहलाता है।
निम्नलिखित प्रश्न को उपयुक्त यूक्लिड की अभिगृहीत का प्रयोग करते हुए, हल कीजिए :
दो सेल्समैन ने अगस्त के महीने में बराबर बिक्री की। सितंबर में, प्रत्येक सेल्समैन अपनी बिक्री अगस्त के महीने की बिक्री की दोगुनी कर लेता है। दोनों की सितंबर की बिक्रियों की तुलना कीजिए।
निम्नलिखित प्रश्न को उपयुक्त यूक्लिड की अभिगृहीत का प्रयोग करते हुए, हल कीजिए :
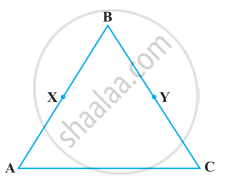
निम्नलिखित आकृति में, हमें प्राप्त है :
BX = `1/2` AB, BY = `1/2` BC तथा AB = BC है। दर्शाइए कि BX = BY है।
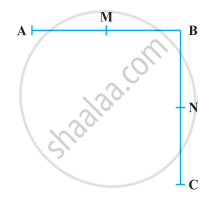
निम्नलिखित आकृति में AB = BC, M रेखाखंड AB का मध्य-बिंदु है और N रेखाखंड BC का मध्य-बिंदु है। दर्शाइए कि AM = NC है।
निम्नलिखित कथन को पढ़िए :
एक समबाहु त्रिभुज तीन रेखाखंडों से बना एक बहुभुज है जिनमें से दो रेखाखंड तीसरे रेखाखंड के बराबर हैं तथा इसका प्रत्येक कोण 60° का है।
इस परिभाषा में, उन पदों को परिभाषित कीजिए जिन्हें आप आवश्यक समझते हैं। क्या इसमें कोई अपरिभाषित पद है? क्या आप इसका औचित्य दे सकते हैं कि एक समबाहु त्रिभुज के सभी कोण और सभी भुजाएँ बराबर होती हैं।
निम्नलिखित कथन का अध्ययन कीजिए :
“दो प्रतिच्छेदी रेखाएँ एक ही रेखा पर लंब नहीं हो सकती हैं।”
जाँच कीजिए कि क्या यह कथन यूक्लिड पाँचवीं अभिधारणा का समतुल्य रूपांतरण है।
[संकेत : उपरोक्त कथन में, दो प्रतिच्छेदी रेखा l और m तथा एक अन्य रेखा n की पहचान कीजिए।]
