Advertisements
Advertisements
प्रश्न
निम्नलिखित प्रश्न को उपयुक्त यूक्लिड की अभिगृहीत का प्रयोग करते हुए, हल कीजिए :
निम्नलिखित आकृति में, ∠ABC = ∠ACB और ∠3 = ∠4 है। दर्शाइए कि ∠1 = ∠2 है।
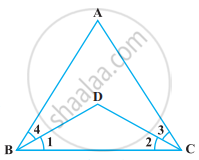
उत्तर
दिया गया है, ∠ABC = ∠ACB ...(i)
और ∠4 = ∠3 ...(ii)
यूक्लिड की अभिगृहीत के अनुसार, यदि बराबर को बराबर में से घटाया जाए, तो शेषफल भी बराबर होता है।
समीकरण (ii) को समीकरण (i) से घटाने पर, हम पाते हैं।
∠ABC – ∠4 = ∠ACB – ∠3
⇒ ∠1 = ∠2
अब, ABDC में, ∠1 = ∠2
⇒ DC = BD ...[समान कोणों की सम्मुख भुजाएँ बराबर होती हैं।]
BD = DC
APPEARS IN
संबंधित प्रश्न
निम्नलिखित पद की परिभाषा दीजिए। क्या इनके लिए कुछ ऐसे पद हैं, जिन्हें परिभाषित करने की आवश्यकता है? वे क्या हैं और आप इन्हें कैसे परिभाषित कर पाएँगे?
वृत्त की त्रिज्या
यदि दो बिंदुओं A और B के बीच एक बिंदु C ऐसा स्थित है कि AC = BC है, तो सिद्ध कीजिए कि AC = `1/2` AB है। एक आकृति खींच कर इसे स्पष्ट कीजिए।
प्राचीन भारत में, आयतों, त्रिभुजों और समलंबों से संयोजित आकारों की वेदियाँ निम्नलिखित में प्रयोग होती थीं :
‘रेखाएँ समांतर होती हैं, यदि वे प्रतिच्छेद नहीं करती’ का कथन, निम्नलिखित के रूप में दिया गया है :
एक पृष्ठ के किनारे वक्र होते हैं।
वे कथन जिन्हें सिद्ध किया जाता है अभिगृहीत कहलाते है।
दो भिन्न प्रतिच्छेदी रेखाएँ एक ही रेखा के समांतर नहीं हो सकतीं।
निम्नलिखित प्रश्न को उपयुक्त यूक्लिड की अभिगृहीत का प्रयोग करते हुए, हल कीजिए :
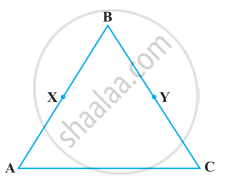
निम्नलिखित आकृति में, हमें प्राप्त है :
BX = `1/2` AB, BY = `1/2` BC तथा AB = BC है। दर्शाइए कि BX = BY है।
निम्नलिखित प्रश्न को उपयुक्त यूक्लिड की अभिगृहीत का प्रयोग करते हुए, हल कीजिए :
निम्नलिखित आकृति में, AC = DC और CB = CE है। दर्शाइए कि AB = DE है।
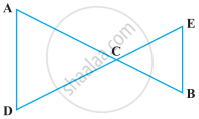
निम्नलिखित कथन को पढ़िए :
एक समबाहु त्रिभुज तीन रेखाखंडों से बना एक बहुभुज है जिनमें से दो रेखाखंड तीसरे रेखाखंड के बराबर हैं तथा इसका प्रत्येक कोण 60° का है।
इस परिभाषा में, उन पदों को परिभाषित कीजिए जिन्हें आप आवश्यक समझते हैं। क्या इसमें कोई अपरिभाषित पद है? क्या आप इसका औचित्य दे सकते हैं कि एक समबाहु त्रिभुज के सभी कोण और सभी भुजाएँ बराबर होती हैं।
