Advertisements
Advertisements
प्रश्न
Obtain an expression for Energy Density of a magnetic field.
उत्तर
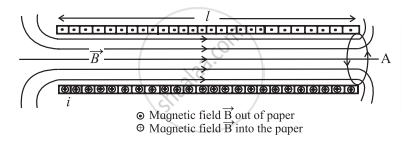
Consider a long solenoid having length, l near the middle, cross-sectional area A and carrying a current i through it. The volume associated with length l will be A.l. The energy stored will be uniformly distributed within the volume, as the magnetic field `barB` is uniform everywhere inside the solenoid. Thus, the energy stored, per unit volume, in the magnetic field is `u_B=U_B/(A.l) ...(1)`
We know energy stored in magnetic field is `u_B=1/2LI^2`
`u_B = 1/2LI^2xx1/(A.l)=(L/l)I^2/(2A) ...(2)`
For a long solenoid, the inductance (L) per unit length is given by,
`(L/l)=mu_0n^2A`
Equation (2) becomes
`u_B=mu_0n^2A.I^2/(2A)`
`=1/2mu_0n^2I^2 ...(3)`
For a solenoid, the magnetic field at the interior points is
`B = mu_0nI`
`u_B=B^2/(2mu_0) ...(4)`
This gives the energy density stored at any point where magnetic field is B.
