Question

Obtain an expression for Energy Density of a magnetic field.

Answer 1

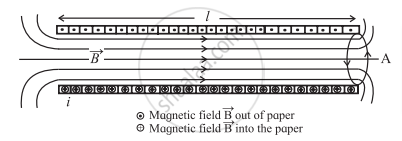
Consider a long solenoid having length, l near the middle, cross-sectional area A and carrying a current i through it. The volume associated with length l will be A.l. The energy stored will be uniformly distributed within the volume, as the magnetic field `barB` is uniform everywhere inside the solenoid. Thus, the energy stored, per unit volume, in the magnetic field is `u_B=U_B/(A.l)           ...(1)`

We know energy stored in magnetic field is `u_B=1/2LI^2`

`u_B = 1/2LI^2xx1/(A.l)=(L/l)I^2/(2A)     ...(2)`

For a long solenoid, the inductance (L) per unit length is given by,

`(L/l)=mu_0n^2A`

Equation (2) becomes

`u_B=mu_0n^2A.I^2/(2A)`

`=1/2mu_0n^2I^2         ...(3)`

For a solenoid, the magnetic field at the interior points is

`B = mu_0nI`

`u_B=B^2/(2mu_0)        ...(4)`

This gives the energy density stored at any point where magnetic field is B.