Question

Obtain the magnetic induction at a point on the equatorial line of a bar magnet. Magnetic field at a point along the equatorial line due to a magnetic dipole (bar magnet).

Answer 1

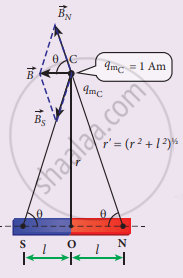
Consider a bar magnet NS. Let N be the north pole and S be the south pole of the bar magnet, each with pole strength q_m and separated by a distance of 2l. The magnetic field at a point C (lies along the equatorial line) at a distance r from the geometrical center O of the bar magnet can be computed by keeping unit north pole (q_mC = 1 A m) at C. The force experienced by the unit north pole at C due to pole strength N-S can be computed using Coulomb’s law of magnetism as follow’s:

The force of repulsion between North Pole of the bar magnet and unit north pole at point C (in free space) is

Magnetic field at a point along the equatorial line due to a magnetic dipole

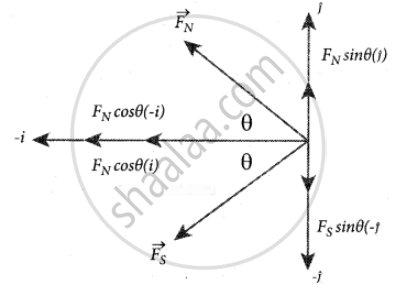
`vec"F"_"N" = - "F"_"N" cos θ  hat"i" + "F"_"N" sin θ  hat "j"`    ....(1)

Where F_N = `mu_0/(4pi)  "q"_"m"/"r'"^2`

The force of attraction (in free space) between south pole of the bar magnet and unit north pole at point C is

`vec"F"_"S" = - "F"_"S" cos θ hat"i" + "F"_"S" sin theta "j"`   .....(2)

where `vec"F"_"S" = mu_0/(4pi)  "q"_"m"/"r'"^2`

From equation (1) and equation (2), the net force at point C is `vec"F" = "F"_"N" + "F"_"S"`

This net force is equal to the magnetic field at point C.

`vec"B" = - ("F"_"N" + "F"_"S") cos theta  hat"i"`

Since, F_N = F_S

Components of force

`vec"B" = - (2mu_0)/(4pi) "q"_"m"/"r'"^2 cos theta  hat"i" = - (2mu_0)/(4pi) "q"_"m"/(("r"^2 + l^2)) cos theta hat"i"`   ....(3)

In a right angle triangle NOC as shown in the Figure.

`cos theta = "adjacent"/"hypotenuse" = 1/"r'" = 1/("r"^2 + l^2)^(1/2)`    ....(4)

Substituting equation 4 in equation 3 We get

`vec"B" = - mu_0/(4pi) ("q"_"m" xx (2l))/("r"^2 + l^2)^(3/2)`     ....(5)

Since, magnitude of magnetic dipole moment is `|vec"P"_"m"| = "P"_"m" = "q"_"m"`.

2l and substituting in equation (5), the magnetic field at a point C is

`vec"B"_"equatorial" = - mu_0/(4pi) "P"_"m"/("r"^2 + l^2)^(3/2) hat "i"`    .....(6)

If the distance between two poles in a bar magnet are small (looks like short magnet) when compared to the distance between geometrical center O of bar magnet and the location of point C i.e., r>> l, then,

`("r"^2 + l^2)^(3/2)`

Therefore, using equation (7) in equation (6), we get ≈ r³ ……… (7)

`vec"B"_"equatorial" = - mu_0/(4pi) "p"_"m"/"r"^3 hat "i"`

Since P_m `hat"i" = |vec"P"_"m"|_"m"`, in general, the magnetic field at equatorial point is given by

`vec"B"_"equatorial" = - mu_0/(4pi) "p"_"m"/"r"^3`    .....(8)

Note that magnitude of `"B"_"axial"` is twice that of magnitude of `"B"_"equatorial"` and the direction of are opposite.