Advertisements
Advertisements
प्रश्न

ऊपर दी गयी आकृति में, ∠ABC यह चाप ABC में अंतर्लिखित कोण है।
यदि ∠ABC = 60%, तो m ∠AOC ज्ञात कीजिए।
हल:
∠ABC =
60° =
परंतु m ∠ AOC = m(चाप
∴ m ∠AOC =
उत्तर
∠ABC =
60° =
120° = m (चाप AXC)
परंतु m ∠ AOC = m(चाप AXC) ......(केंद्रीय कोण का गुणधर्म)
∴ m ∠AOC = 120°
APPEARS IN
संबंधित प्रश्न
संलग्न आकृति में, जीवा EF || जीवा GH तो सिद्ध कीजिए कि, जीवा EG ≅ जीवा FH नीचे दी गई उपपत्ति में रिक्त स्थानों की पूर्ति कर उपपत्ति पूर्ण कीजिए।
उपपत्ति : रेख GF खींचिए।
∠EFG = ∠FGH ...........
∠EFG =
∠FGH =
∴ m (चाप EG) =
जीवा EG ≅ जीवा FH ..........
दी गई आकृति में, जीवा PQ तथा जीवा RS एक-दूसरे को बिंदु T पर प्रतिच्छेदित करती हैं। यदि ∠STQ = 58° तथा ∠PSR = 24° हो, ही तो निम्न कृति पूर्ण करके सिद्ध करो:
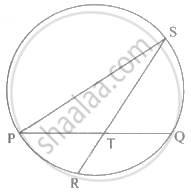
∠STQ =
कृति: ΔPTS में,
∠STQ = ∠STQ –
∠SPQ = 34°
m(चाप QS) = 2 ×
उसी प्रकार, m(चाप PR) = 2∠PSR =
परंतु, ∠STQ = 58° .............. (2) (दिया है।)
∴
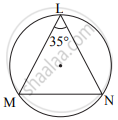
ऊपर दी गई आकृति में, ∠L = 35° तो
- m(चाप MN)
- m(चाप MLN)
ज्ञात कीजिए।
हल:
- ∠L =
∴
∴ 2 × 35 = m(चाप MN)
∴ m(चाप MN) = - m(चाप MLN) =
= 360° - 70°
∴ m(चाप MLN) =
