Advertisements
Advertisements
प्रश्न
PQRS is a parallelogram and O is any point in its interior. Prove that: area(ΔPOQ) + area(ΔROS) - area(ΔQOR) + area(ΔSOP) = `(1)/(2)`area(|| gm PQRS)
उत्तर
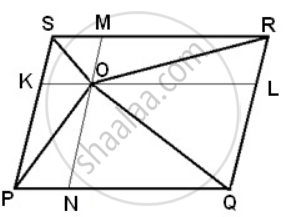
Let us draw a line segment KL, Passing through point O and parallel to line segment PQ.
In parallelogram PQRS,
PQ || KL ...(By construction) ...(1)
PQRS is a parallelogram.
∴ PS || QR ...(Opposite sides of a parallelogram)
⇒ PK || Ql ...(2)
From equation (1) and (2), we obtain
PQ || KL and PK || QL
Therefore, quadrilateral PQLK is a parallelogram.
It can be observed that ΔPOQ and parallelogram PQLK are lying on the same base PQ and between the same parallel lines PK and QL.
∴ Area(ΔPOQ) = `(1)/(2)`Area (parallelogram PQLK) ...(3)
Similarly, for ΔROS and parallelogram KLRS,
Area(ΔROS) = `(1)/(2)`Area (parallelogram KLRS) ...(4)
Adding equations (3) and (4), we obtain
Area(ΔPOQ) + Area(ΔROS)
= `(1)/(2)"Area (parallelogramm PQLK)" + (1)/(2) "Area (parallelogram KLRS)"`
Area(ΔPOQ) + Area(ΔROS) = `(1)/(2)"Area (PQRS)"` ......(5)
Let us draw a line segment MN, passing through point OP and parallel to line segment PS.
In parallelogram PQRS,
NN || PS ...(By construction) ...(6)
PQRS is a parallelogram.
∴ PQ || RS ...(Opposite sides of a parallelogram)
⇒ PN || SN ...(7)
From equations () and (7), we obtain
MN || PSannd PN || SN
Therefore, quadrilateralPNMS is a parallelogram.
It can be observed that ΔPOS and parallelogram PNMS are lying on the same base PS and between the same parallel lines PS and MN.
∴ Area(ΔSOP) = `(1)/(2)"Area (PNMS)"` ...(8)
Similarly, for ΔQOR and parallelogram MNQR,
Area(ΔQOR) = `(1)/(2)"Area (MNQR)"` ...(9)
Adding equations (8) and (9), we obtain
Area(ΔSOP) + Area(ΔQOR)
= `(1)/(2)"Area (PNMS)" + (1)/(2)"Area (MNQR)"`
Area(ΔSOP) + Area(ΔQOR) = `(1)/(2)"Area (PQRS)"` ..........(10)
On comparing equation (5) and (10), we obtain
Area(ΔPOQ) + Area(ΔROS)
= Area(ΔSOP) + Area(ΔQOR)
= `(1)/(2)`Area (|| gm PQRS)`.
APPEARS IN
संबंधित प्रश्न
SN and QM are perpendiculars to the diagonal PR of parallelogram PQRS.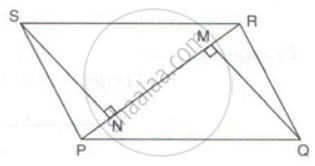
Prove that:
(i) ΔSNR ≅ ΔQMP
(ii) SN = QM
ABCD is a parallelogram. P and T are points on AB and DC respectively and AP = CT. Prove that PT and BD bisect each other.
PQRS is a parallelogram. PQ is produced to T so that PQ = QT. Prove that PQ = QT. Prove that ST bisects QR.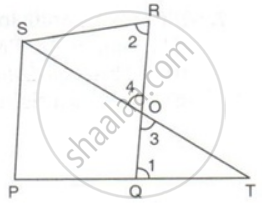
ABCD is a rectangle with ∠ADB = 55°, calculate ∠ABD.
ABCD is a quadrilateral P, Q, R and S are the mid-points of AB, BC, CD and AD. Prove that PQRS is a parallelogram.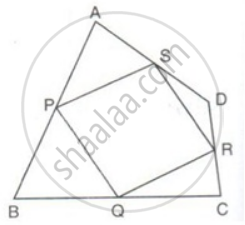
In a parallelogram PQRS, M and N are the midpoints of the opposite sides PQ and RS respectively. Prove that
RN and RM trisect QS.
In a parallelogram PQRS, M and N are the midpoints of the opposite sides PQ and RS respectively. Prove that
PMRN is a parallelogram.
In the given figure, PQRS is a parallelogram in which PA = AB = Prove that: SA ‖ QB and SA = QB.
In the given figure, PQRS is a trapezium in which PQ ‖ SR and PS = QR. Prove that: ∠PSR = ∠QRS and ∠SPQ = ∠RQP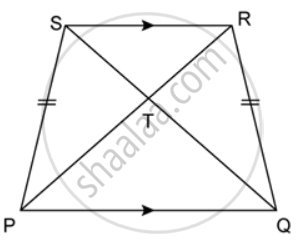
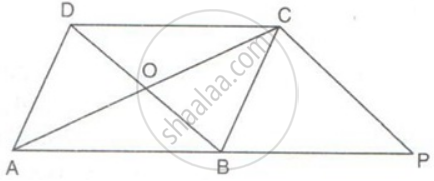
In the figure, ABCD is a parallelogram and CP is parallel to DB. Prove that: Area of OBPC = `(3)/(4)"area of ABCD"`