Advertisements
Advertisements
प्रश्न
In a parallelogram PQRS, M and N are the midpoints of the opposite sides PQ and RS respectively. Prove that
RN and RM trisect QS.
उत्तर
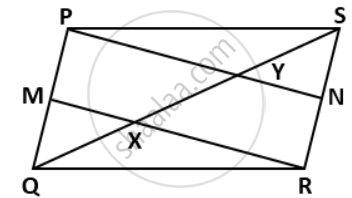
Since M and N are the mid-point of PQ and RS respectively.
∴ PM = `(1)/(2)"PQ" and "RN" = (1)/(2)"RS"` ....(i)
But PQRS is a parallelogram,
∴ PQ = RS and PQ || RS
⇒ `(1)/(2)"PQ" = (1)/(2)"RS"` and PQ || RS
⇒ PM = RN and PQ || RS
⇒ PMRN is a parallelogram.
⇒ PN || RM
⇒ NY || RX ....(ii)
We know that the segment drawn through the mid-point of one side of a triangle and parallel to the other side bisects the third side.
In ΔSRX, N is the mid-point of RS and NY || RX ....[From (ii)]
∴ Y is the mid-point of QY
⇒ XY = YS ....(iii)
Similarly, in ΔPQY, M is the mid-point of PQ and MX || PY ....[From (ii)]
⇒ QX = XY ....(iv)
From (iii) and (iv), we get
QX = XY = YS
⇒ X and Y trisect QS
⇒ PN and RM trisect QS.
APPEARS IN
संबंधित प्रश्न
Prove that if the diagonals of a parallelogram are equal then it is a rectangle.
ABCD is a quadrilateral P, Q, R and S are the mid-points of AB, BC, CD and AD. Prove that PQRS is a parallelogram.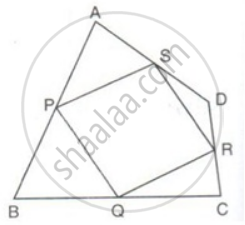
PQRS is a parallelogram. T is the mid-point of RS and M is a point on the diagonal PR such that MR = `(1)/(4)"PR"`. TM is joined and extended to cut QR at N. Prove that QN = RN.
Prove that the line segment joining the mid-points of the diagonals of a trapezium is parallel to each of the parallel sides, and is equal to half the difference of these sides.
In a parallelogram PQRS, M and N are the midpoints of the opposite sides PQ and RS respectively. Prove that
MN bisects QS.
ABCD is a trapezium in which side AB is parallel to side DC. P is the mid-point of side AD. IF Q is a point on the Side BC such that the segment PQ is parallel to DC, prove that PQ = `(1)/(2)("AB" + "DC")`.
In the given figure, PQRS is a parallelogram in which PA = AB = Prove that: SAQB is a parallelogram.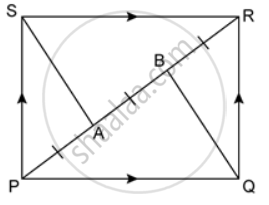
Prove that the diagonals of a square are equal and perpendicular to each other.
In ΔPQR, PS is a median. T is the mid-point of SR and M is the mid-point of PT. Prove that: ΔPMR = `(1)/(8)Δ"PQR"`.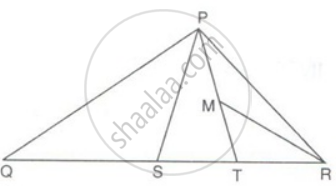
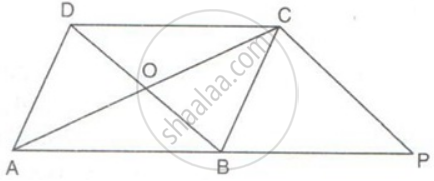
In the figure, ABCD is a parallelogram and CP is parallel to DB. Prove that: Area of OBPC = `(3)/(4)"area of ABCD"`