Advertisements
Advertisements
Question
In a parallelogram PQRS, M and N are the midpoints of the opposite sides PQ and RS respectively. Prove that
RN and RM trisect QS.
Solution
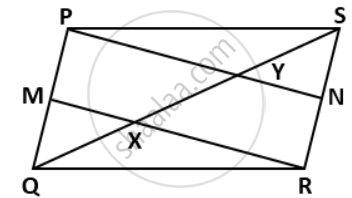
Since M and N are the mid-point of PQ and RS respectively.
∴ PM = `(1)/(2)"PQ" and "RN" = (1)/(2)"RS"` ....(i)
But PQRS is a parallelogram,
∴ PQ = RS and PQ || RS
⇒ `(1)/(2)"PQ" = (1)/(2)"RS"` and PQ || RS
⇒ PM = RN and PQ || RS
⇒ PMRN is a parallelogram.
⇒ PN || RM
⇒ NY || RX ....(ii)
We know that the segment drawn through the mid-point of one side of a triangle and parallel to the other side bisects the third side.
In ΔSRX, N is the mid-point of RS and NY || RX ....[From (ii)]
∴ Y is the mid-point of QY
⇒ XY = YS ....(iii)
Similarly, in ΔPQY, M is the mid-point of PQ and MX || PY ....[From (ii)]
⇒ QX = XY ....(iv)
From (iii) and (iv), we get
QX = XY = YS
⇒ X and Y trisect QS
⇒ PN and RM trisect QS.
APPEARS IN
RELATED QUESTIONS
ABCD is a parallelogram. P and Q are mid-points of AB and CD. Prove that APCQ is also a parallelogram.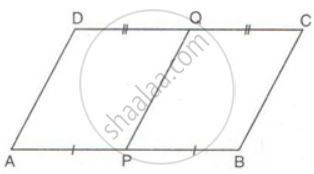
SN and QM are perpendiculars to the diagonal PR of parallelogram PQRS.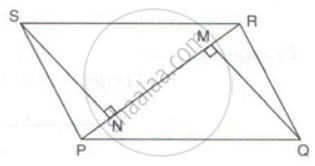
Prove that:
(i) ΔSNR ≅ ΔQMP
(ii) SN = QM
PQRS is a parallelogram. PQ is produced to T so that PQ = QT. Prove that PQ = QT. Prove that ST bisects QR.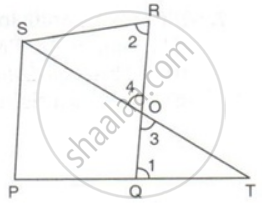
ABCD is a quadrilateral P, Q, R and S are the mid-points of AB, BC, CD and AD. Prove that PQRS is a parallelogram.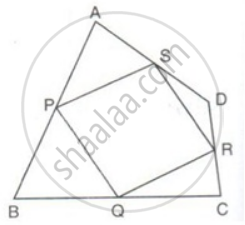
In a parallelogram PQRS, M and N are the midpoints of the opposite sides PQ and RS respectively. Prove that
PMRN is a parallelogram.
In the given figure, PQRS is a parallelogram in which PA = AB = Prove that: SA ‖ QB and SA = QB.
In the given figure, PQRS is a parallelogram in which PA = AB = Prove that: SAQB is a parallelogram.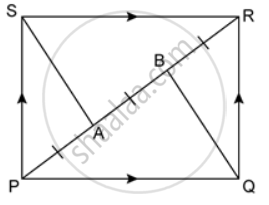
Prove that the diagonals of a kite intersect each other at right angles.
In the given figure, PQ ∥ SR ∥ MN, PS ∥ QM and SM ∥ PN. Prove that: ar. (SMNT) = ar. (PQRS).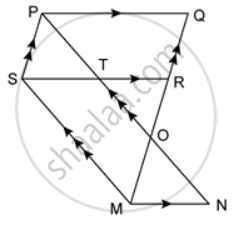
In ΔABC, the mid-points of AB, BC and AC are P, Q and R respectively. Prove that BQRP is a parallelogram and that its area is half of ΔABC.
