Advertisements
Advertisements
Question
In the given figure, PQ ∥ SR ∥ MN, PS ∥ QM and SM ∥ PN. Prove that: ar. (SMNT) = ar. (PQRS).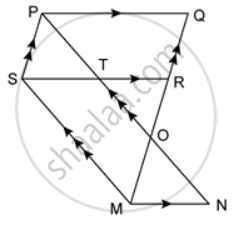
Solution
SM ∥ PN
⇒ SM ∥ TN
Also, SR ∥ MN
⇒ ST ∥ MN
Hence, SMNT is a parallelogram.
SM ∥ PN
⇒ SM ∥ PO
Also, PS ∥ QM
⇒ PS ∥ OM
Hence, SMOP is a parallelogram.
Now, parallelograms SMNT and SMOP are on the same base SM and between the same parallels SM and PN.
∴ A(parallelogram SMNT) = A(parallelogram SMOP) ….(i)
Similarly, we can show that quadrilaterals PQRS is a parallelogram.
Now, parallelograms PQRS and SMOP are on the same base PS and between the same parallels PS and QM.
∴ A(parallelogram PQRS) = A(parallelogram SMOP) ….(ii)
From (i) and (ii), we have
A(parallelogram SMNT) = A(parallelogram PQRS).
APPEARS IN
RELATED QUESTIONS
ABCD is a parallelogram. P and Q are mid-points of AB and CD. Prove that APCQ is also a parallelogram.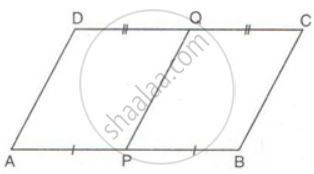
SN and QM are perpendiculars to the diagonal PR of parallelogram PQRS.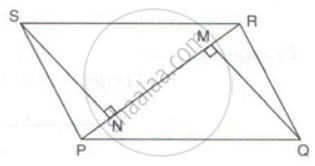
Prove that:
(i) ΔSNR ≅ ΔQMP
(ii) SN = QM
ABCD is a parallelogram. P and T are points on AB and DC respectively and AP = CT. Prove that PT and BD bisect each other.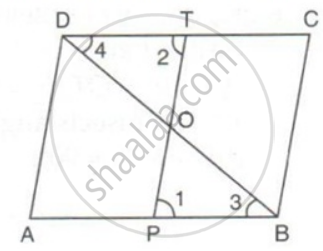
ABCD is a rectangle with ∠ADB = 55°, calculate ∠ABD.
ABCD is a quadrilateral P, Q, R and S are the mid-points of AB, BC, CD and AD. Prove that PQRS is a parallelogram.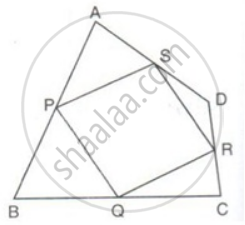
In the given figure, PQRS is a parallelogram in which PA = AB = Prove that: SAQB is a parallelogram.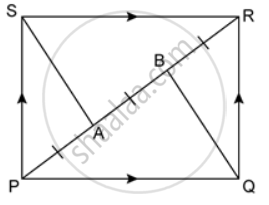
In the given figure, PQRS is a trapezium in which PQ ‖ SR and PS = QR. Prove that: ∠PSR = ∠QRS and ∠SPQ = ∠RQP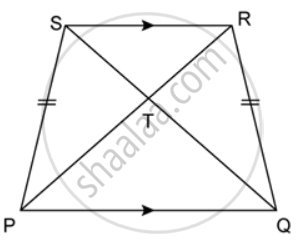
The diagonals AC and BC of a quadrilateral ABCD intersect at O. Prove that if BO = OD, then areas of ΔABC an ΔADC area equal.
In the given figure, AB ∥ SQ ∥ DC and AD ∥ PR ∥ BC. If the area of quadrilateral ABCD is 24 square units, find the area of quadrilateral PQRS.
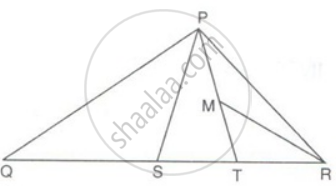
In ΔPQR, PS is a median. T is the mid-point of SR and M is the mid-point of PT. Prove that: ΔPMR = `(1)/(8)Δ"PQR"`.