Advertisements
Advertisements
Question
The diagonals AC and BC of a quadrilateral ABCD intersect at O. Prove that if BO = OD, then areas of ΔABC an ΔADC area equal.
Solution
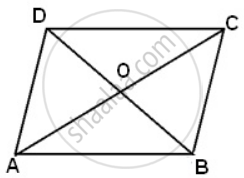
In ΔABD,
BO = OD
⇒ O is the mid-point of BD
⇒ AO is a median.
⇒ ar(ΔAOB) = ar(ΔAOD) ..........(i)
In ΔCBD, O is the mid-point of BD
⇒ CO is a median.
⇒ ar(ΔCOB) = ar(ΔCOD) ..........(ii)
Adding (i) and (ii)
ar(ΔAOB) 6 ar(ΔCOB) = ar(ΔAOD) + ar(ΔCOD)
Therefore, ar(ΔABC) = ar(ΔADC).
APPEARS IN
RELATED QUESTIONS
PQRS is a parallelogram. T is the mid-point of RS and M is a point on the diagonal PR such that MR = `(1)/(4)"PR"`. TM is joined and extended to cut QR at N. Prove that QN = RN.
P is a point on side KN of a parallelogram KLMN such that KP : PN is 1 : 2. Q is a point on side LM such that LQ : MQ is 2 : 1. Prove that KQMP is a parallelogram.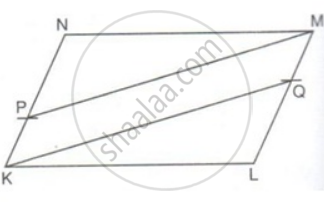
Prove that the line segment joining the mid-points of the diagonals of a trapezium is parallel to each of the parallel sides, and is equal to half the difference of these sides.
In a parallelogram PQRS, M and N are the midpoints of the opposite sides PQ and RS respectively. Prove that
MN bisects QS.
In the given figure, PQRS is a parallelogram in which PA = AB = Prove that: SAQB is a parallelogram.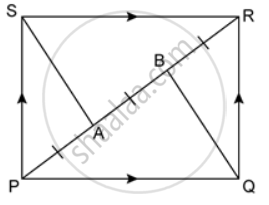
In the given figure, PQRS is a trapezium in which PQ ‖ SR and PS = QR. Prove that: ∠PSR = ∠QRS and ∠SPQ = ∠RQP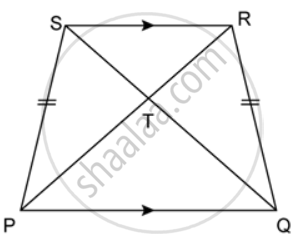
Prove that the diagonals of a kite intersect each other at right angles.
In the given figure, PQ ∥ SR ∥ MN, PS ∥ QM and SM ∥ PN. Prove that: ar. (SMNT) = ar. (PQRS).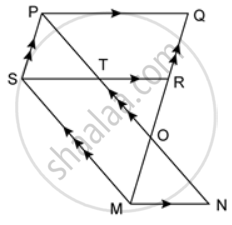
In the figure, ABCD is a parallelogram and CP is parallel to DB. Prove that: Area of OBPC = `(3)/(4)"area of ABCD"`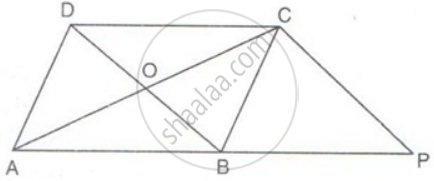
The medians QM and RN of ΔPQR intersect at O. Prove that: area of ΔROQ = area of quadrilateral PMON.
