Advertisements
Advertisements
Question
Prove that the line segment joining the mid-points of the diagonals of a trapezium is parallel to each of the parallel sides, and is equal to half the difference of these sides.
Solution
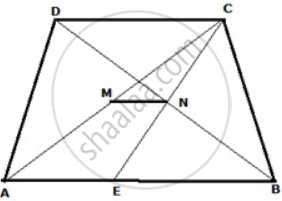
Join AC and BD. M and N are mid-points of AC and BD respectively. Join MN. Draw a line CN cutting AB at E.
Now, in Δs DBC and BNE,
DN = NB ...(N is the mid-point of BD, given)
∠CDB = ∠EBN ...(Alternate angles as DC || AB)
∠DNC = BNE ...(Vertically opposite angles)
⇒ ΔDNC ≅ ΔBNE ...(By A-S-A Test)
⇒ DC = BE
By Mid-point Theorem, in ΔACE, M and N are mid-points
MN = `(1)/(2)"AE" and "MN" || "AE" or "MN" || "AB"`
Also, AB || CD, therefore, MN || CD
⇒ MN = `(1)/(2)["AB" = "BE"]`
⇒ MN = `(1)/(2)["AB" = "CD"]` ...(since BE = CD)
⇒ MN = `(1)/(2)` x Difference of parallel sides AB and CD.
APPEARS IN
RELATED QUESTIONS
SN and QM are perpendiculars to the diagonal PR of parallelogram PQRS.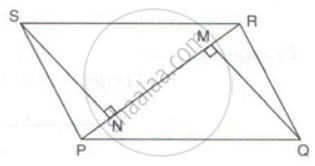
Prove that:
(i) ΔSNR ≅ ΔQMP
(ii) SN = QM
ABCD is a parallelogram. P and T are points on AB and DC respectively and AP = CT. Prove that PT and BD bisect each other.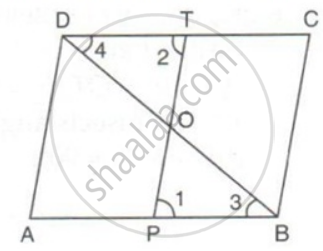
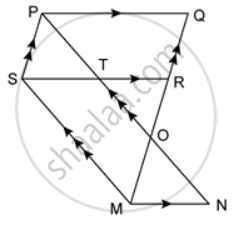
PQRS is a parallelogram. T is the mid-point of RS and M is a point on the diagonal PR such that MR = `(1)/(4)"PR"`. TM is joined and extended to cut QR at N. Prove that QN = RN.
In a parallelogram PQRS, M and N are the midpoints of the opposite sides PQ and RS respectively. Prove that
PMRN is a parallelogram.
In the given figure, PQRS is a parallelogram in which PA = AB = Prove that: SAQB is a parallelogram.
In the given figure, PQRS is a trapezium in which PQ ‖ SR and PS = QR. Prove that: ∠PSR = ∠QRS and ∠SPQ = ∠RQP
Prove that the diagonals of a kite intersect each other at right angles.
The diagonals AC and BC of a quadrilateral ABCD intersect at O. Prove that if BO = OD, then areas of ΔABC an ΔADC area equal.
PQRS is a parallelogram and O is any point in its interior. Prove that: area(ΔPOQ) + area(ΔROS) - area(ΔQOR) + area(ΔSOP) = `(1)/(2)`area(|| gm PQRS)
In the given figure, PQ ∥ SR ∥ MN, PS ∥ QM and SM ∥ PN. Prove that: ar. (SMNT) = ar. (PQRS).