Advertisements
Advertisements
Question
In the given figure, PQRS is a trapezium in which PQ ‖ SR and PS = QR. Prove that: ∠PSR = ∠QRS and ∠SPQ = ∠RQP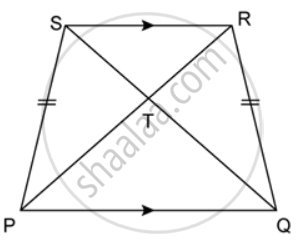
Solution
Construction:
Draw SM ⊥ PQ and RN ⊥ PQ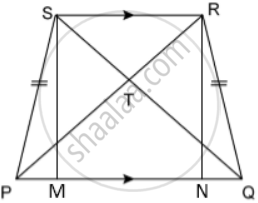
a. In ΔPMS and ΔQNR,
PS = QR ....(given)
∠PMS = ∠QNR ....(Each 90°)
SM = RN ....(Distance between parallel lines)
∴ ΔPMS ≅ ΔQNR ....(RHS congruence)
⇒ ∠PM = ∠RQN
⇒ ∠SPQ = ∠RQP
⇒ ∠PSR = ∠QRS ....(Supplement of each angle SPQ and RQP)
b. In ΔPQS and ΔQPR,
PS = QR ....(given)
∠SPQ = ∠RQP ....(proved)
PQ = PQ ....(common)
∴ ΔPQS ≅ ΔQPR ....(SAS congruence)
⇒ QS = PR ....(proved)
⇒ PSQ = ∠QRP ....(i)
c. In ΔTPS and ΔTQR,
PS = QR ....(given)
∠STP = ∠RTQ ....(Vertically opposite angles)
∠PST = ∠QRT ....[From (i)]
∴ ΔTPS ≅ ΔTQR ....(SAS congruence)
⇒ TP = TQ ....(proved)
⇒ TS = TR. ....(proved)
APPEARS IN
RELATED QUESTIONS
ABCD is a parallelogram. P and T are points on AB and DC respectively and AP = CT. Prove that PT and BD bisect each other.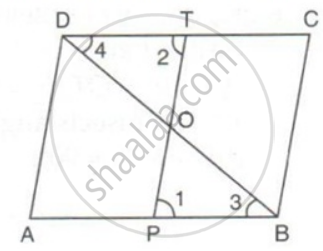
ABCD is a rectangle with ∠ADB = 55°, calculate ∠ABD.
PQRS is a parallelogram. T is the mid-point of RS and M is a point on the diagonal PR such that MR = `(1)/(4)"PR"`. TM is joined and extended to cut QR at N. Prove that QN = RN.
P is a point on side KN of a parallelogram KLMN such that KP : PN is 1 : 2. Q is a point on side LM such that LQ : MQ is 2 : 1. Prove that KQMP is a parallelogram.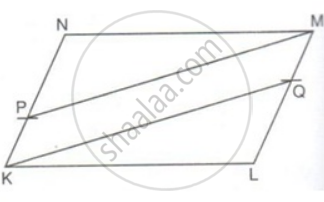
In the given figure, PQRS is a parallelogram in which PA = AB = Prove that: SA ‖ QB and SA = QB.
Prove that the diagonals of a kite intersect each other at right angles.
Prove that the diagonals of a square are equal and perpendicular to each other.
In the given figure, AB ∥ SQ ∥ DC and AD ∥ PR ∥ BC. If the area of quadrilateral ABCD is 24 square units, find the area of quadrilateral PQRS.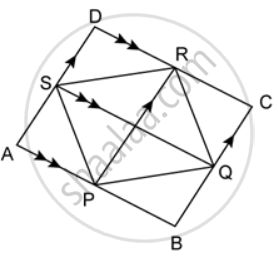
In the given figure, PQ ∥ SR ∥ MN, PS ∥ QM and SM ∥ PN. Prove that: ar. (SMNT) = ar. (PQRS).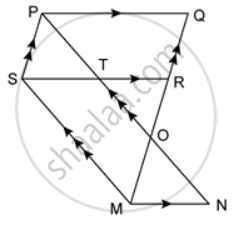
In ΔABC, the mid-points of AB, BC and AC are P, Q and R respectively. Prove that BQRP is a parallelogram and that its area is half of ΔABC.
